Les travaux de Grégory Miermont, médaille d’argent CNRS 2018

Grégory Miermont est professeur à l’École Normale Supérieure de Lyon depuis 2012 et actuellement membre junior de l’IUF. Il a soutenu sa thèse à l’Université Pierre et Marie Curie en 2003 sous la direction de Jean Bertoin, puis il a été chargé de recherche au CNRS à l’Université Paris Sud Orsay et à l’École Normale Supérieure de la rue d’Ulm entre 2004 et 2009, avant de devenir Professeur à l’Université Paris Sud, puis de muter à Lyon.

Ses premiers pas de chercheur ont été l’occasion de résoudre et clarifier de nombreuses questions naturelles reliées aux structures aléatoires branchantes (arbres, processus de fragmentation-coagulation).

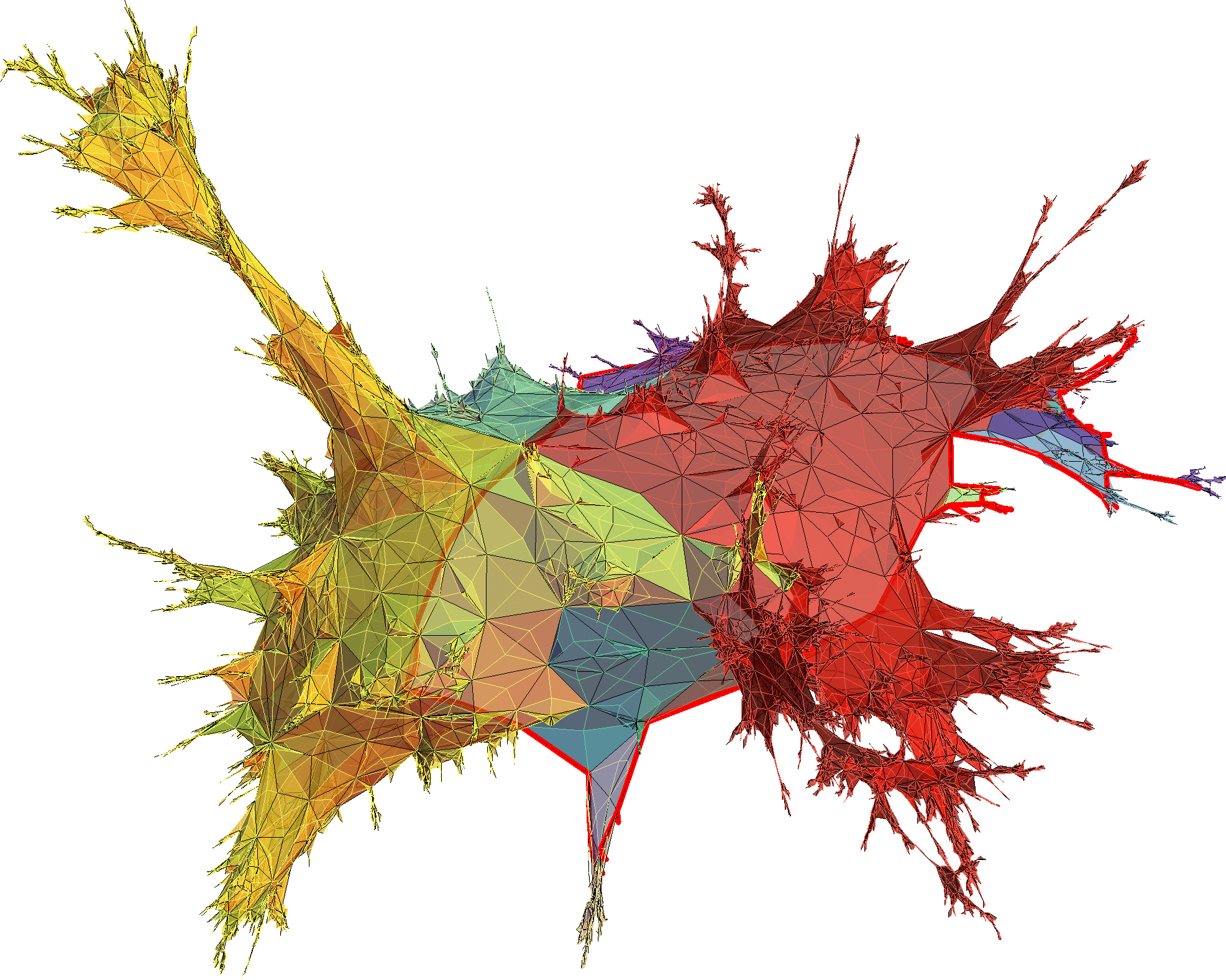
Ces dernières années, son effort de recherche a porté sur l’étude des cartes planaires, un domaine en plein développement qui se trouve à l’interface entre combinatoire, physique théorique et probabilités. Il s’agit de comprendre les propriétés à grande échelle de graphes plans (définis suivant des règles très simples – par exemple, on fixe le nombre de nœuds, et on choisit uniformément au hasard un graphe dessiné dans le plan, où chaque face est bordé par quatre arêtes – c’est une quadrangulation, et où deux graphes sont identifiés s’il existe un homéomorphisme du plan permettant de passer de l’un à l’autre). Une motivation importante vient du fait que de tels graphes sont supposés permettre de modéliser les fluctuations autour d’une métrique euclidienne et que les modèles physiques sur ces graphes (Ising, percolation etc.) sont supposés exhiber des comportements universels remarquables. Ils sont par ailleurs plus accessibles que l’étude de modèles sur des graphes réguliers habituels, car ils possèdent des propriétés combinatoires remarquables. On peut aussi noter que l’étude d’intégrales matricielles (à la Itzykson, Brézin, Zuber) était initialement motivée par ces questions de cartes planaires.

L’une des propriétés combinatoires remarquables de ces cartes planaires est qu’il existe des bijections entre certains ensembles de cartes et des ensembles correspondants d’arbres étiquetés. Via ces bijections, l’étude asymptotique de grandes cartes planaires peut être abordée grâce à des considérations sur le comportement de grandes structures arborescentes aléatoires. Grégory Miermont a su exploiter ces relations de manière particulièrement spectaculaire, et il a obtenu des résultats marquants : l’universalité (le fait que différents modèles de cartes donnent lieu à la même structure continue limite), l’étude et la compréhension de cartes sur des surfaces de genre arbitraire, etc.

En 2011, Grégory Miermont a résolu le problème ouvert principal dans le sujet, à savoir la convergence des quadrangulations aléatoires vers un espace métrique aléatoire « continu » (appelé la carte brownienne, [3] ; ce résultat a été obtenu de manière indépendante, par des méthodes différentes par Jean- François Le Gall). C’est l’un des résultats les plus importants en théorie des probabilités obtenus pendant ces dernières années.

Dans les années récentes, Grégory Miermont a obtenu d’autres résultats importants dans le domaine de la géométrie aléatoire. On peut citer en particulier son travail avec Bettinelli sur les disques browniens (un analogue « avec frontière » de la carte brownienne, [4]), son long article avec Baur et Ray [5] qui classifie toutes les limites possibles de quadrangulations avec frontière, ou encore son beau travail avec Addario-Berry, Broutin et Goldschmidt sur la limite d’échelle de l’arbre couvrant minimal sur le graphe complet [6].