Ecoulements granulaires et mouvements de foules

C’est dans cet esprit qu’a été développé le code de calcul SCoPI (Simulation de Collections de Particules en Interaction) qui permet la simulation de grains rigides en interaction interne (forces interparticulaires, contacts secs ou lubrifiés) ou externe (obstacles de différents types, prise en compte de forces extérieures, fluide porteur …), mais également la modélisation de mouvements de foules humaines ou de cellules vivantes.

L’origine : simulation d’écoulements granulaires

Le développement de ce code a démarré en 2005 lors de la thèse d’Aline Lefebvre-Lepot (soutenue en 2007), au Laboratoire de Mathématiques d’Orsay, et il a permis de simuler des écoulements granulaires 2D ou 3D avec des collisions entre grains rigides soit inélastiques soit suivant le modèle de contact visqueux développé par Bertrand Maury [Ma07]. Dès le départ il semblait évident que l’outil développé allait devoir être capable de supporter au fil des années l’ajout de nouveaux types d’obstacles, de nouveaux modèles de contact ou encore de permettre l’utilisation de différents algorithmes de résolutions de systèmes linéaires. En conséquence, le choix d’un langage orienté objet, en l’occurrence le C++ pour SCoPI, a semblé naturel et un important travail de conception des différents objets a été effectué avant d’écrire la moindre ligne de code. Cette réflexion s’est appuyée sur des travaux précédemment réalisés au Laboratoire de Mathématiques d’Orsay dans le cadre du projet CSiMoon [LLL04] qui propose une méthodologie orientée objet capable de garantir, pour un cahier des charges donné et dans un contexte de calcul scientifique, les notions d’évolution, d’efficacité, de modularité, de structuration de la programmation et d’optimisation.
 

Extension aux mouvements de foules

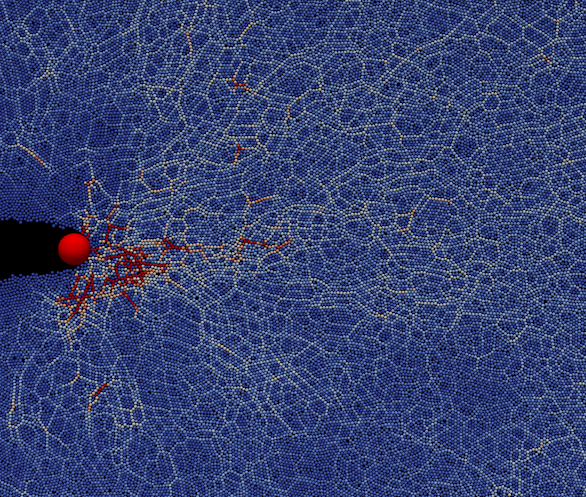
Ce procédé de développement a facilité l’ajout de nouvelles fonctionnalités initialement prévues (nouveaux obstacles en mouvement, interface graphique permettant une visualisation temps réel, parallélisation des opérations les plus coûteuses) mais également d’étendre l’éventail des fonctionnalités à des problématiques non initialement envisagées, en particulier dans le domaine de la simulation de mouvements de foules. Si l’on identifie des personnes dans un bâtiment à des disques rigides, le fait que deux personnes ne peuvent pas être au même endroit au même moment s’exprime comme la contrainte de non-chevauchement entre grains rigides. Il est alors possible de modéliser les mouvements complexes d’une foule en mouvement en considérant que chaque individu a une vitesse souhaitée (qu’il prendrait s’il était tout seul), et que la vitesse effective de la foule (ou plus précisément de la collection de disques) est définie comme la vitesse admissible (c’est à dire ne violant pas la contrainte de non chevauchement) la plus proche de la vitesse souhaitée globale. Juliette Venel dans le cadre de sa thèse (soutenue en 2008) a ainsi pu ajouter tous les objets nécessaires à la simulation de phénomènes d’évacuation de foule [MV07], [MV10], [Ma14].

Avenir

Avec SCoPI, il est aujourd’hui possible de simuler des écoulements granulaires secs, des mouvements de foules dans un contexte d’évacuation de bâtiments mais également de prévoir le comportement d’écoulements de fluides complexes grâce au couplage avec des solveurs fluides (grains rigides immergés dans un fluide [FGM13]). Concernant les écoulements, les simulations réalisées sont motivées par des collaborations avec des physiciens du FAST à Orsay afin de pouvoir comparer les résultats numériques avec des expériences réalisées en laboratoire. Dans ce cas il s’agit de travaux visant à étudier le comportement (vitesse d’écoulement, stabilité, viscosité…) de milieux granulaires ou de suspensions. Aussi bien industriels (retraitement des déchets nucléaires, bétons, plastiques renforcés), que naturels (sable, envasement, eaux claires) ou biologiques (tests sanguins), les domaines d’application sont nombreux… Quant aux mouvements de foule, après avoir fait de nombreux calculs montrant la pertinence des modèles utilisés, il s’agit maintenant d’arriver à se confronter à des données réelles, par exemple des flux piétonniers dans une gare, afin d’améliorer les modèles et de pouvoir se rapprocher d’utilisateurs potentiels.