Maths & Musique #2 : Mathématiques de l'accord des claviers, par Dominique Manchon

1. Les instruments à clavier

Le clavier d’un piano moderne est constitué de 88 touches, réparties entre 52 touches blanches consécutives et 36 touches noires qui viennent s’intercaler entre les blanches, suivant un motif périodique. En parcourant tout le clavier de gauche à droite, on rencontre d’abord le motif initial BNBBNBNB, puis le motif central1

BNBNBNBBNBNB

répété six fois, et enfin le motif final BNBNBNBB.

• 1Un bon moyen de se rappeler ce motif de douze lettres est de faire défiler les mois de l’année de janvier à décembre. Les touches blanches correspondent exactement aux mois de 31 jours, les touches noires aux mois courts.

Les claviers des orgues, clavecins, épinettes, les claviers des pianos, et de nos jours les claviers électroniques, sont de longueur variable, mais adoptent tous cette structure essentiellement immuable depuis le XV^ème siècle2 . Chaque touche correspond à l’émission d’un son ayant une hauteur bien définie, une note de musique. Le motif central décrit la gamme chromatique

Fa Fa# Sol Sol# La La# Si Do Do# Ré Ré# Mi

du grave vers l’aigu. Les touches noires sont figurées en gras. La touche blanche suivante est encore un Fa, formant un intervalle d’une octave avec le premier Fa, et le motif se répète à chaque octave.

Pourquoi y a-t-il douze notes dans une octave, disposées de cette manière, et comment accorde-t-on les instruments à clavier ? Pour donner quelques éléments de réponses à ces très vastes questions, le bon point de départ réside dans la nature du son. Sur un instrument à cordes, une note de musique correspond à la vibration d’une corde avec une fréquence bien déterminée : par exemple, le troisième Fa en partant de la gauche vibre environ 176 fois par seconde (176 Hertz). Le Fa suivant vibre à la fréquence double, soit 352 fois par seconde.

2. Le cycle des quintes

On a remarqué depuis plus de 2 500 ans, avec Pythagore, que lorsque le rapport entre deux fréquences s’exprime comme le quotient de deux entiers positifs suffisamment petits, l’intervalle formé par ces deux fréquences est consonant. En se limitant aux nombres entre 1 et 2, le rapport le plus simple après 1 (l’unisson) et 2 (l’octave) est 3/2, l’intervalle correspondant s’appelle la quinte juste. On trouve ensuite la quarte représentée par 4/3, la sixte majeure (5/3), la tierce majeure (5/4), la tierce mineure (6/5), la sixte mineure (8/5), la septième mineure (9/5),…

Si on double l’intervalle de quinte, il faut multiplier 3/2 avec lui-même, ce qui donne 9/4=2,25. Autrement dit, deux quintes superposées forment un intervalle un peu plus grand que l’octave. Que se passe-t-il lorsque l’on continue à empiler des quintes successives ? En multipliant 3/2 douze fois par lui-même, on obtient (3/2)¹² = 129,746… C’est assez proche de 2⁷ = 128. Autrement dit, il y a à peu près douze quintes dans sept octaves. En répartissant douze notes dans une octave, la quinte correspond donc à un intervalle comprenant sept notes.

Partons du premier Fa tout à gauche du clavier (la première touche blanche du motif central le plus à gauche), et montons vers l’aigu en frappant une note sur sept. Nous obtenons la suite

Fa Do Sol Ré La Mi Si Fa# Do# Sol# Ré# La# (Fa)

qui se répartit sur toute l’étendue du clavier, et même un peu au-delà : le dernier Fa entre parenthèses vibre à environ 5632 Hz, 128 fois plus vite que le Fa de départ (44 Hz), et excède les limites du clavier d’un piano, il est figuré là pour refermer le cycle :

• 2A ma connaissance, la plus ancienne représentation d’un clavier semblable au clavier moderne se trouve dans un traité d’Arnaut de Zwolle, daté approximativement de 1440.

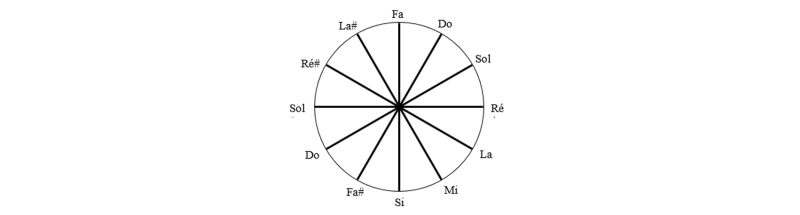
Les nombres 7 et 12 étant premiers entre eux, les douze notes sont toutes représentées dans cette suite. On remarque que les sept premières notes correspondent aux touches blanches, les touches noires n’arrivant qu’après.

Nous pouvons donc fixer les fréquences de toutes les notes en partant d’un Fa de référence, et en accordant successivement toutes les octaves et toutes les quintes. Dans la pratique, par exemple, on part d’un Fa au milieu du clavier, on accorde le Do à la quinte au-dessus3 . On répète l’opération avec le Sol au-dessus du Do, et on accorde ensuite l’octave entre ce Sol et celui juste en-dessous, puis on accorde la quinte Sol-Ré, etc. En continuant ce processus, on parvient ainsi à accorder les douze notes du Fa de départ au Mi juste au-dessus, en terminant par le La#. On accorde alors la totalité du clavier en réglant les octaves.

3. La quinte du loup et le comma enharmonique

Mais ce n’est pas si simple ! Cet accord, dit  pythagoricien, révèle ses faiblesses lorsque l’on teste la dernière quinte La# Fa4  (rappelons que le Fa est donné dès le départ), qui s’avère vraiment fausse ! Cela n’a rien d’étonnant : on a vu que 12 quintes ne rentrent pas tout-à-fait dans 7 octaves, la dernière quinte se trouve donc sensiblement rabotée. L’erreur se mesure par le rapport

K=(3/2)¹²/2⁷ = 3¹²/2¹⁹ = 1.01364…

Cet intervalle s’appelle le comma enharmonique. Bien que très petit, il est parfaitement audible.

4. Comment accorder un clavier : le tempérament

Les théoriciens et les accordeurs ont très vite eu l’idée de répartir ce défaut sur plusieurs quintes au lieu de le concentrer sur une seule. Dès la fin du XVIe siècle Simon Stevin, précédé de quelques décennies par les Chinois, propose de raboter chaque quinte d’un douzième du comma enharmonique K. Douze de ces quintes un peu raccourcies font exactement sept octaves. Deux touches consécutives sont toujours séparées par un demi-ton tempéré qui vaut exactement un douzième d’octave, soit un rapport de 2^1/12=1,05946… Le tempérament égal était né ! Il domine toute la vie musicale occidentale depuis un bon siècle, mais il ne s’est imposé qu’au prix d’une forte et longue résistance. Des centaines de tempéraments inégaux ont coexisté avec lui pendant des siècles, dont certains sont toujours utilisés en musique ancienne.

5. La tierce majeure et le comma syntonique

En ajoutant une quarte (représentée par le rapport de fréquences 4/3) à une quinte, on obtient une octave. C’est la traduction musicale de la simple égalité (3/2)x(4/3)=2. Après la quinte et la quarte, l’intervalle consonant suivant est la tierce majeure, correspondant au rapport 5/4. Par ailleurs, en effectuant quatre quintes successives on obtient un intervalle représenté par le rapport 81/16. En lui retranchant deux octaves on arrive à 81/64, assez proche de 5/4=80/64. Cet intervalle, appelé diton ou tierce majeure pythagoricienne, sonne assez durement à l’oreille. L’erreur est mesurée par le comma syntonique représenté par le rapport k=81/80=1,0125. Il donc est proche du comma enharmonique K=1,01364… mais un peu plus petit. La différence entre les deux intervalles, représentée par le rapport 𝜎=K/k, est le schisma, qui peut s’identifier à K^1/12 avec une excellente approximation : la différence entre le douzième de comma enharmonique (que nous noterons r par commodité) et le schisma est un intervalle minuscule et parfaitement indétectable5 .

6. Conclusion : imaginez votre tempérament

• 3à l’oreille, une quinte un peu fausse fait entendre de lentes oscillations, les battements. L’accordeur ajuste la tension de manière à ce que les battements disparaissent, obtenant ainsi une quinte juste.
• 4C’est plus précisément une sixte diminuée, mais ne pinaillons pas…
• 5Représenté par le rapport de fréquences k/(K^{11/12})=1,0000007394… C’est le douzième d’un atome de Kirnberger, appelé d’après son découvreur Johann Philipp Kirnberger (1721-1783). Il se représente par le rapport k^{12}/K^{11}= 2^{161}3^{-84}5^{-12}= 1,00000887286…
  Le lecteur attentif aura remarqué que nous sommes souvent passés de la multiplication à l’addition et vice-versa. L’addition de deux intervalles se traduit en effet par la multiplication de leurs rapports de fréquences respectifs. On passe facilement d’un point de vue à l’autre par l’utilisation du logarithme en base 2.

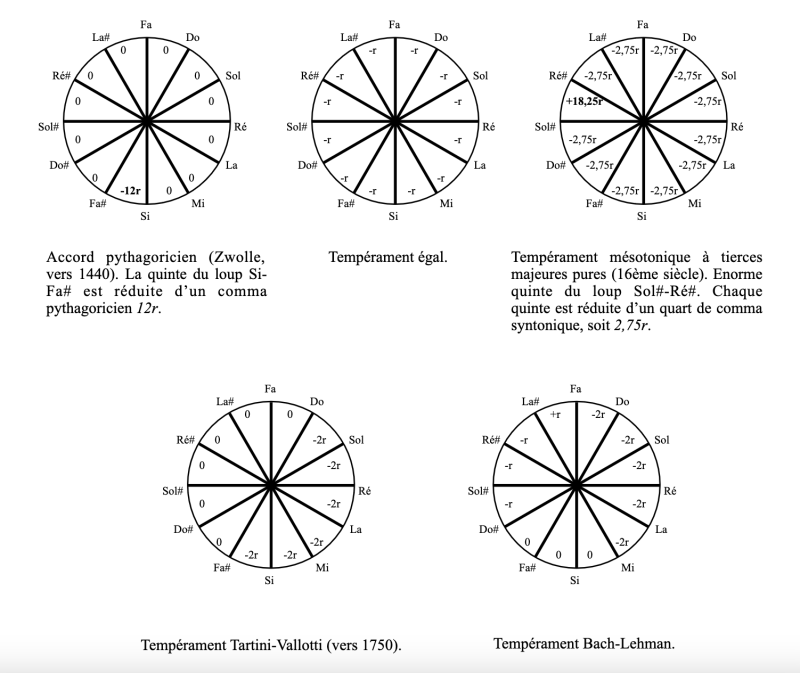
En résumé, il faut retrancher un comma enharmonique (soit 12r) au cycle des quintes pour pouvoir le boucler, ce comma étant à répartir entre les douze quintes du cycle. Par ailleurs, il faut retrancher un comma syntonique (soit presque exactement 11r) à une tierce pythagoricienne pour obtenir une tierce majeure pure.

Dans le tempérament égal, les tierces majeures sont toutes égales, raccourcies de 4r par rapport à la tierce majeure pythagoricienne, mais excédant encore de 7r la tierce majeure pure. Dans tout tempérament, cet excès de 7r par rapport à la tierce majeure pure est toujours vérifié en moyenne. La différence avec le tempérament égal réside dans un autre choix pour la répartition des erreurs. Supposons par exemple que nous souhaitions obtenir une tierce majeure pure Fa-La. On peut pour ce faire raccourcir les quatre quintes Fa-Do, Do-Sol, Sol-Ré et Ré-La de 11r/4=2,75r. On peut choisir de raccourcir toutes les quintes (sauf la dernière) de cette valeur 2,75r : c’est le tempérament mésotonique à tierces majeures pures, qui convient particulièrement bien à la musique de la Renaissance. Le prix à payer pour toutes ces belles tierces majeures est une énorme quinte du loup (excédant de 18,25r la quinte pure), interdisant de jouer dans certaines tonalités.

L’exercice se complique encore lorsque l’on prend en compte la tierce mineure représentée par le rapport de fréquences 6/5. La prise en compte d’intervalles consonants plus exotiques comme la septième naturelle (7/4) ou la onzième naturelle (11/4) est impossible sauf énorme déformation des autres intervalles. La justesse d’un instrument à clavier sera toujours une affaire de compromis.

Pour aller plus loin

Le site de Bradley Lehman fournit une description très complète d’un très beau tempérament qui est peut-être celui préconisé par J. S. Bach pour son Clavier Bien Tempéré6 . Pour une présentation générale d’un grand nombre de tempéraments anciens, le livre de Pierre-Yves Asselin (Musique et tempérament, Editions Jobert, Paris, 2000) est une très bonne introduction. Je recommande aussi l’excellent site de Gunnar Tungland, inventeur d’une très belle représentation graphique des tempéraments. Sur les petits et très petits intervalles mentionnés dans cet article, voir le récent post de John Baez sur The n-category café.

• 6Ce point a fait l’objet de nombreuses et vives controverses. Difficile d’affirmer que B. Lehman a effectivement découvert le tempérament utilisé par Bach, mais l’auteur de cet article l’a adopté avec bonheur sur tous ses instruments à clavier !