Maths & Musique #5 : Le tempérament musical revisité, par Laurent Mazliak

Lire l'article intégral sur Arts et Sciences

Le système des tonalités est celui sur lequel la musique occidentale s’est développée pendant des siècles. La question du tempérament musical traverse l’histoire de la musique occidentale depuis longtemps car elle surgit d'un problème très concret : comment accorder un instrument à clavier (positifs, orgues, clavecins, piano…). L’exemple le plus emblématique et le plus célèbre est sans nul doute donné par Jean-Sébastien Bach et son « clavier bien tempéré », œuvre théorique où le compositeur allemand a voulu illustrer comment le choix adéquat d’un tempérament pour le clavier pouvait permettre une circulation satisfaisante entre les différentes tonalités majeures ou mineures. 

Rappelons quelques éléments de base sur ce problème, puis nous commenterons la très originale exploitation du tempérament que propose le compositeur contemporain hongrois György Ligeti dans le premier mouvement de sa sonate pour alto seul.

Considérons une corde de guitare. Le son qu'elle émet quand on la pince est une vibration périodique de l'air à une fréquence f. En fait, les savants des 17ème et 18ème siècle (notamment Mersenne et d'Alembert) ont montré que cette vibration est la juxtaposition d'une infinité de vibrations (dites harmoniques) dont les fréquences de vibrations sont les multiples entiers de f : 2f, 3f, 4f etc. On sait aussi que la fréquence du son émis est inversement proportionnelle à la longueur de la corde : par exemple, en mettant son doigt au milieu de la corde, on obtiendra une note de fréquence 2f ; en le mettant aux 1/3 de la longueur, on laisse vibrer les 2/3 de la corde et on obtient une note de fréquence 3/2f etc.

La vibration de fréquence 2f « épouse » très bien la vibration de fréquence f, le cerveau concevant ces deux sons comme très proches: on dit qu'ils sont distants d'une octave et les notes musicales correspondantes sont désignées par le même nom. La vibration qui vient ensuite est celle de fréquence 3f. Comme 3f = 2. (3/2 f), on voit que la note correspondante est la même que celle de fréquence 3/2.f : on l'appelle la quinte (ascendante).

Partant d’un son de fréquence f, en multipliant la fréquence à chaque fois par 3/2, on peut donc construire une suite de sons distants les uns des autres d’une quinte ascendante :

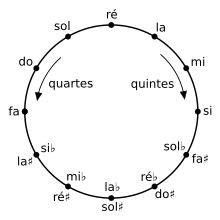
Cette construction (dite cycle des quintes) contient a priori une infinité de sons dont aucun n’est distant d’une ou plusieurs octaves d’un autre car aucune puissance de 3 n'égale une puissance de 2. Mais il se passe un phénomène intéressant car (3/2)¹² = 129,74… est plutôt proche de 2⁷ = 128. Si on « fait comme si » les deux notes de fréquence (3/2)¹² f et 2⁷f  sont identiques, on peut poser mi# = fa. Une conséquence est que le cycle des quintes se referme et qu’on peut considérer l’ensemble des douze notes construites plus haut (qu’on qualifie de total chromatique) comme un ensemble clos pour le passage de quinte en quinte. En regardant les douze notes construites, on montre qu’on peut diviser leur fréquence par une puissance de 2 adéquate pour obtenir une fréquence entre f et 2f et on obtient l'ordre suivant :

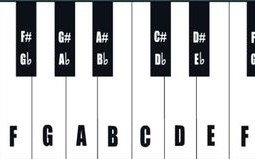
Ces douze notes constituent la frise qui va se répéter d'octave en octave sur un instrument à clavier.

Mais nous avons triché en considérant (3/2)¹² et 2⁷ comme étant égaux et il va falloir tenir compte de cette erreur pour accorder ces douze sons. Une option est de répartir l’erreur uniformément sur les 12 intervalles, ce qu’on appelle le tempérament égal. Mais ce choix est totalement artificiel : les rapports « naturels » de quinte ont purement et simplement disparu, ce qui fait que, pour ainsi dire, tout sonne (un peu) faux…. D'infinies possibilités s’offrent en fait aux accordeurs pour répartir l’erreur. 

La question du tempérament musical n’est véritablement cruciale que pour les instruments avec clavier. Sur un instrument comme le violon, la musicienne ou le musicien peut placer son doigt sur la corde à d’autres endroits qu’à la moitié, au tiers, au quart… Avec une grande originalité, Ligeti a revisité la question sur un instrument sans clavier : un alto. Pour donner au premier mouvement Hora Lunga de sa sonate pour alto seul, une atmosphère évoquant la musique folklorique de Transylvanie, Ligeti invente un système de répartition des sons fondé sur les déviations des fréquences par rapport au tempérament égal.

Imaginons une corde de fréquence fondamentale fa. En effleurant avec son doigt la corde à des endroits spécifiques, l’interprète peut jouer des harmoniques qui ont une fréquence plus ou moins déviée par rapport à la fréquence obtenue en tempérament égal. Seulement, une grosse difficulté apparaît :  il n'y a pas de corde de fa sur un alto. Du coup, Ligeti demande à l'interprète un tour de force : dans la première moitié de la pièce, il doit calquer sur la corde de do (sur laquelle l'ensemble de la pièce doit être exécutée) la répartition des différentes notes avec des déviations correspondant à celles de la corde fictive de fa. Ligeti indique donc sur la partition les notes sur lesquelles opérer des déviations (mesurées en cents) :

Pour réaliser ces notes, l’altiste doit recourir à diverses méthodes qui peuvent être panachées :

• accorder la corde de sol de l’alto un ton plus grave, pour qu’elle produise un fa et en écouter les harmoniques naturelles ;

• produire des harmoniques artificielles en appuyant de façon fixe avec un doigt la corde sur la note fondamentale souhaitée (selon le principe du capodastre sur une guitare) et en effleurant d’un autre doigt de la même main les nœuds qui lui sont accessibles. Sur un instrument comme un alto, en fonction de la taille de leur main, les interprètes ont la possibilité de reproduire avec cette technique les notes dès la deuxième harmonique. Mais celles au-delà de la 5ème s’avèrent quasiment impossible à faire sonner ;

• transposer (par imitation des écarts) sur l’échelle de fa les sonorités des harmoniques naturelles entendues sur une autre corde ;

• faire appel à une tierce personne qui, pour faire sonner les harmoniques, va effleurer la corde alors que l’interprète conservera la fondamentale appuyée (ou inversement).