Maths & Music #3: Music, word combinatorics and computer improvisation, by Marc Chemillier
Music has always been closely linked to mathematics. From the5th century BC onwards, the Pythagoreans began to explore the relationship between music and numbers.

Much closer to home, Joseph Fourier (1768-1830) laid the foundations of harmonic analysis by studying certain periodic signals such as sound waves. In the 20th century, the development of computer science introduced a completely new field of mathematical study of music, with very powerful concepts such as word combinatorics, which we will discuss here. These enable us to design musical software that radically changes the way we make music.
In theoretical computer science, we study sequences of symbols called words on an alphabet. These are abstract symbols that can be actions to be executed in a program when it comes to computer science, but also musical notes or any other object, depending on the field of application studied. This concept is well suited to describing the succession of events within a musical sequence, just as it is to describing and controlling the sequence of syntactic units in a language from a computational linguistics perspective.
When it comes to sequences of symbols, one of the simplest things you can think of is the repetition of elements in the sequence. For example, a "square" is the repetition of a pattern stated twice consecutively as (abc)(abc). Can we construct a sequence with a two-letter alphabet a and b that contains no squares? We start by placing an a. We can't place a second one, because we'd have the square (a)(a), so we place a b to form ab. Next, we must place an a to form aba, otherwise we'd have the square (b)(b). You can't extend aba, because if you place an a, the square (a)(a) appears, and if you place a b, the square (ab)(ab) appears. We've just proved that it's impossible to construct a word without a square if the alphabet has only two letters. However, it is possible as soon as the alphabet has at least three letters. With two letters, it's possible to construct words without a cube (i.e., without a pattern stated three times consecutively). Norwegian mathematician Axel Thue (1863-1922) discovered one such cube that extends to infinity. He described it in a 1912 paper considered to be the foundation of word combinatorics, along with another paper by him dating from 1906.
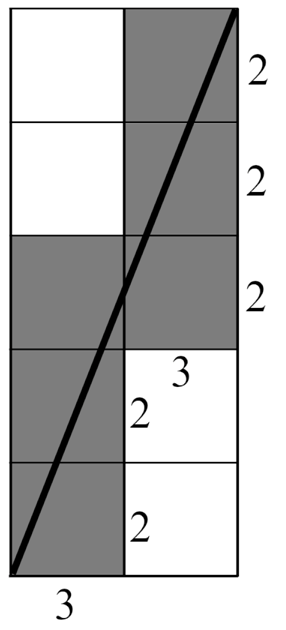
In music, the succession of all available notes, ascending or descending, produces what's known as a scale. For example, the succession of white keys on a piano is the diatonic scale (starting from the note C). It has very special mathematical properties, linked to the fact that the black keys separating the white keys are placed irregularly, two on one side and three on the other. In fact, if we consider the intervals between the white keys, we have two semitones between C and D, then two semitones between D and E, but only one semitone between E and F. On all the white keys of the keyboard, we obtain the interval sequence 2212221, which is a word on the alphabet with two symbols 1 and 2. This word has the following remarkable property: there is a rotation 2221221 which is palindrome if its two initial and final symbols 2(22122)1 are removed. In fact, the bracketed pattern 22122 gives the same succession of digits in either direction.
What's even more surprising is that a similar property is obtained by taking the complementary keys, i.e. those that are black. The corresponding scale interval sequence called pentatonic is the word 23223 on alphabet 2 and 3. Here again, there is a rotation 22323 which is palindrome, except for the first and last symbols 2(232)3. But that's not all: the same phenomenon can also be observed in rhythm. You're probably familiar with the song "Djadja" by Aya Nakamura. It's based on a rhythm called reggaeton, very common in today's popular music, which can be written 332 (two dotted eighth notes followed by one eighth note). It's also the rhythm of the "Bande organisée" rap. It comes from a family of asymmetrical African rhythms that have been studied by ethnomusicologist Simha Arom 332, 32322, 3223222 and so on. What do these rhythms have in common? They can all be written as 32n32n+1, if 2n is the sequence of 2s repeated n times. They contain a very long square (32n)(32n), but their distribution is asymmetrical because there's an extra 2 on the right, extending the second occurrence of the square. All these words are palindromes when the two symbols at the ends 3(2n32n)2 are removed.
In mathematics, these rhythms or scales are related to what are known as Christoffel words, in honor of the mathematician Elwin Christoffel (1829-1900), who first studied them in an 1875 article in which he observed their palindrome character. It is astonishing to find these sequences in fields as varied as Western scales and African rhythms, all the more so as the latter are based on a strictly oral tradition. The study of such unwritten structures is the subject of ethnomathematical research. There are two opposing approaches in this field. One, based on the decolonization of knowledge, considers that these structures cannot be compared with those of the written tradition, because they appear in contexts that are too different. The other, more universalist, view is that the same structures appear because the combinatorial principles on which they are based are the same, whether in terms of alternating intervals in the scale, or durations in the rhythms. This is the second point of view adopted in this article.
Let's turn now to the music creation software we talked about at the beginning. One of the revolutions in artificial intelligence in recent decades has been the development of machine learning algorithms. In music, a computer can capture a musician's playing and then, based on this data, create music all by itself. One of the reasons for this prodigy is that the recorded data already contains an enormous amount of implicit musical knowledge, such as the musician's phrasing, timbre, articulation and expression. A similar situation arose with sampling, which made it possible to recycle musical fragments that were themselves already highly elaborate. But with learning-based artificial intelligence, this phenomenon is multiplied tenfold by its generative dimension.
The most widely studied models at present are those of deep learning based on connectionist networks, but other simpler symbolic models, less costly in terms of computing resources, can prove to be extremely effective. One of the first generative models based on transition probabilities was introduced in 1913 by Andrei Markov (1856-1922) in connection with a statistical study of a literary text.
Let's take the abracadabra sequence as an example. The a can be followed by three letters b, c or d, but it's more likely to be followed by b than by the other two. On the other hand, r, c and d are always followed by a, and b is always followed by r. If we generate a new word by randomly drawing according to these weighted rules, the result will be limited to permutations of the syllables bra, ca and da. Thus, the generative capacity of training data depends on the repetitions it contains, i.e. its redundancy. The idea of repetition is echoed in the words developed earlier about word combinatorics. Some words allow more generative variants than others. These learning techniques are used in software for musical improvisation developed as part of the ERC REACH project (IRCAM and CAMS) directed by Gérard Assayag. In these musical applications, the letters forming the words can be signal slices (between 2 dates in milliseconds) associated with different metadata (harmonics, for example). They can be used to capture a musician's playing and create a kind of computer double that can dialogue live with the musician. The computer can also improvise from large databases of solos by great masters of improvisation and play in their style, or hybridize several styles together.

One of the improvisation software programs we're working on, called Djazz, is being used to explore the following question: can an artificial intelligence system learn to play in the musical style of a given culture to the point of being able to integrate itself into a local orchestra or ritual? This is possible with Djazz, as the software performs what is described as agnostic supervised learning, i.e. it makes no a priori assumptions about the musical knowledge involved - apart from a few very simple ones, such as the existence of a regular pulse (necessary for dance music, for example). We used Djazz in different contexts, and the idea that the software could learn to play in a musician's style took on a particular resonance. Indeed, one of the musicians we worked with in Madagascar, Velonjoro, passed away in 2017. But in 2022, another great Malagasy musician Justin Vali wanted to play a duet with him. This was virtually possible thanks to Velonjoro's playing data stored in the computer.

Contact
To find out more:
- Marc Chemillier's personal page
- Editorial and list of Maths & Musique articles
- Livre-CD Artisticiel. Cyber-improvisations, by Bernard Lubat, Gérard Assayag, Marc Chemillier, Phonofaune, 2021.
- Justin Vali meets Jacek Woźniak show, Festival de l'imaginaire, June 8, 2023.
