Des systèmes dynamiques faiblement chaotiques
Les systèmes dynamiques physiques décrits par des lois d’évolution déterministes sont souvent extrêmement complexes. Pour les étudier, il est parfois possible de montrer que leur comportement est très semblable à celui d’un système aléatoire. Dans certains cas, ce système aléatoire peut même être considéré comme proche d’un système où les positions successives sont tirées au hasard indépendamment les unes des autres. Cette description n’est jamais parfaitement exacte, mais si le système initial est suffisamment chaotique (on parle souvent d’effet papillon pour le grand public, alors que les mathématiciens parlent de mélange exponentiel), on peut démontrer que cette approximation est suffisamment bonne pour que nombre de résultats probabilistes classiques s’appliquent à notre système physique initial déterministe, et permettent de décrire son comportement de manière satisfaisante pour la plupart des conditions initiales. Dans un article récent, J. Dedecker, S. Gouëzel et F. Merlevède s’intéressent à des systèmes dynamiques plus complexes à analyser car leurs propriétés chaotiques sont faibles : bien que ces systèmes soient mélangeants, ce mélange est lent, si bien qu’il subsiste des corrélations fortes entre les configurations du système en différents instants (on parle de « courte mémoire » ou de « longue mémoire » en fonction de l’intensité de ces corrélations). Dans les deux régimes, les auteurs sont capables d’évaluer la quantité de trajectoires dont le comportement est exceptionnel par rapport au comportement moyen du système. Leur résultat montre la pertinence et la puissance de l’outil probabiliste dans l’analyse des systèmes dynamiques.
Le texte ci-dessous (hormis les simulations, qui ont été réalisées pour l'occasion) présente certains résultats de l'article [2].
Les chaînes de Markov non irréductibles apparaissent naturellement lorsque l'on étudie certains systèmes dynamiques d'un point de vue probabiliste. L'exemple typique est celui d'une transformation dilatante $T$ de l'intervalle $[0,1]$, pour laquelle il existe une unique probabilité invariante $\nu$ absolument continue par rapport à la mesure de Lebesgue. Dans ce cas l'opérateur de Perron-Frobenius $K$ de $T$ pour $\nu$, à savoir l'adjoint dans ${\mathbb L}^{2} (\nu)$ de l'opérateur de Koopman $P_T$ associé à $T$ défini par $P_Tf:=f\circ T$, est un noyau de transition Markovien admettant $\nu$ pour mesure invariante. Il est alors (d'un point de vue probabiliste) équivalent d'étudier les itérations de $T$ sur $([0,1], \nu)$ ou la chaîne stationnaire de noyau $K$.
Dans ce contexte, les probabilités de transition associées à $K$ et la mesure $\nu$ sont singulières, et la chaîne n'est pas irréductible, i.e. il existe un ensemble Borélien $B$ de mesure $\nu(B)>0$ qui ne soit pas accessible depuis tout point de départ. L'existence de petits ensembles accessibles n'est alors pas garantie et les techniques de régénération en cycles indépendants ne sont pas applicables. Cela implique en particulier que les nombreux résultats connus pour les chaînes irréductibles (par exemple les chaînes $\alpha$-mélangeantes au sens de Rosenblatt [5] ne s'appliquent pas.
Pour traiter ces exemples, une des façons de procéder est d'évaluer le "mélange" de ces chaînes sur des classes d'observables bornées "régulières" en un certain sens, plutôt que de considérer toutes les classes observables bornées comme c'est le cas pour le $\alpha$-mélange.
D'un point de vue formel, considérons une chaîne de Markov stationnaire $(X_i)_{i \geq 0}$ d'espace d'états ${\mathcal X}$, de noyau $K$ et de mesure invariante $\nu$. Soit $({\mathcal B}, \|\cdot \|)$ un sous-espace de fonctions bornées de ${\mathcal X}$ dans ${\mathbb R}$, la norme $\|\cdot \|$ étant telle que $\|f\|_\infty \leq C \|f\|$ (pour $C>0$) et $\|f \cdot g\| \leq \|f\|\|g\|$. Soit $p>1$, et supposons que l'opérateur $K$ vérifie les conditions suivantes : il existe une constante $C_1>0$ telle que, pour toute fonction $f \in {\mathcal B}$ et tout $n\geq 1$,
$$ \nu \left ( \left |K^n(f) - \pi (f)\right | \right ) \leq \frac{C_1\|f\|}{n^{p-1}} \, ; (1)
$$
il existe une constante $C_2>0$ telle que, pour toute fonction $f \in
{\mathcal B}$ et tout $n\geq 1$,
$$
\|K^n (f)\| \leq C_2 \|f\|\, . (2)
$$
On notera $H(p)$ l'ensemble des deux conditions (1) et (2). On dira alors que la chaîne mélange lentement (par opposition à une vitesse de décroissance géométrique dans (1)). Notons que si ${\mathcal B}$ est l'espace des fonctions mesurables bornées muni de la norme $\|\cdot \|_\infty$, alors (2) est toujours vraie, et la chaîne est $\alpha$-mélangeante au sens de Rosenblatt si elle satisfait (1).
Si l'on s'intéresse aux probabilités de moyennes et grandes déviations des sommes d'observables de la chaîne, on montre que si (1) et (2) sont vraies, alors, pour toute $f \in {\mathcal B}$, il existe $C>0$ ne dépendant que de $p$ et de $\|f\|$ telle que, pour tout $x>0$ et tout $\alpha \in (1/2, 1]$ tel que $\alpha \geq 1/p$,
$$
\limsup_{n \rightarrow \infty} n^{\alpha p -1} {\mathbb P}\left (
{\max_{1 \leq k \leq n} \left |\sum_{i=1}^k (f(X_i) - \nu(f) ) \right |
\geq x n^{\alpha}}\right ) \leq \frac{C}{x^p} \, . (3)
$$
De plus, on peut exhiber des exemples de chaînes, d'espaces ${\mathcal B}$ et d'observables $f \in {\mathcal B}$ montrant que la vitesse $n^{\alpha p -1} $ et la "fonction de taux" $x\rightarrow x^{-p}$ ne peuvent pas être améliorées dans (3).
Pour illustrer ce résultat général, considérons la famille des transformations intermittentes de $[0,1]$ introduites par Liverani, Saussol et Vaienti [4] : pour $\gamma \in ]0,1[$,
$$T_\gamma(x)=
\begin{cases}
x(1+ 2^\gamma x^\gamma) \quad \text{ si $x \in [0, 1/2[$}\\
2x-1 \quad \quad \quad \ \ \text{si $x \in [1/2, 1]$.}
\end{cases}$$
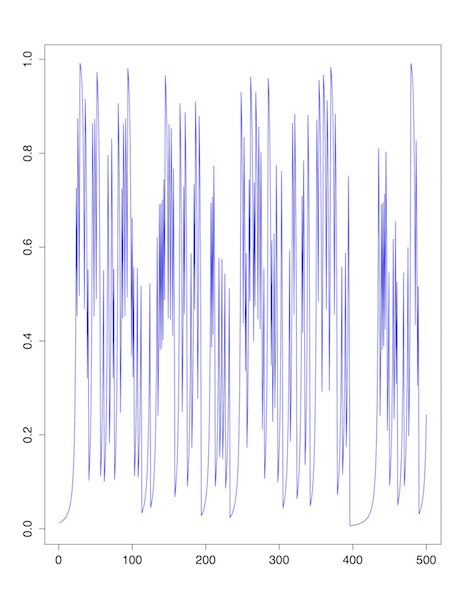
Sur la figure 1, on peut observer le comportement intermittent des itérées de $T_\gamma$ : soit chaotique, car $T_\gamma$ est dilatante avec une dérivée strictement plus grande que 1 sauf en 0, soit quasiment constant et proche de 0, car 0 est un point fixe neutre de $T_\gamma$. Le comportement chaotique
est d'autant plus marqué que $\gamma$ est proche de 0 ($T_0$ est uniformément dilatante), et les périodes où les itérées sont quasiment nulles ont tendance à être de plus en plus longues lorsque $\gamma$ se rapproche de 1.
La transformation $T_\gamma$ admet une unique probabilité invariante $\nu_\gamma$ absolument continue par rapport à la mesure de Lebesgue (voir [4]). On peut montrer que l'opérateur de Perron-Frobenius de $T_\gamma$ par rapport à la mesure $\nu_\gamma$ satisfait (1) et (2) pour $p=1/\gamma$ et ${\mathcal B}$ l'espace des fonctions à variation bornées de [0,1] (voir [1]). En revanche, la condition (2) n'est pas vraie si ${\mathcal B}$ est l'espace des fonctions Hölderiennes de [0,1]; mais dans ce cas, on peut utiliser le codage par une tour de Young [6], et montrer que (1) et (2) sont vraies pour l'opérateur adjoint sur la tour. En conclusion, on obtient que si $f$ est soit Hölderienne (quelque soit l'exposant dans ]0,1]), soit à variation bornée, il existe $C>0$ dépendant de $f$ et de $\gamma$ telle que, pour tout $x>0$ et tout $\alpha \in (1/2, 1]$ tel que $\alpha \geq \gamma$,
$$
\limsup_{n \rightarrow \infty} n^{\alpha/\gamma -1} {\nu_\gamma}\left (
{\max_{1 \leq k \leq n} \left |\sum_{i=1}^k (f \circ T^i_{\gamma}
- \nu_\gamma(f) ) \right |
\geq x n^{\alpha}}\right ) \leq \frac{C}{x^{1/\gamma}} \, .
\quad\quad\quad (4)
$$
Simulations
On prend d'abord $\gamma=\alpha=3/4$, de sorte que la vitesse dans (3) vaut $n^{\alpha/\gamma -1}=1$. On simule $N=2000$ fois les sommes $S_n(y)=\sum_{i=1}^n ( T^i_{3/4} - \nu_{3/4}(\text{Id}))(y)$ avec $y$ tiré uniformément sur [0, 0.05], pour différentes valeurs de $n$ : 500, 1000, 1500, 2000. Les quatre boîtes à
moustache des 4$\times 2000$ tirages de $n^{-3/4}S_n(y)$ sont présentées ci-dessous.
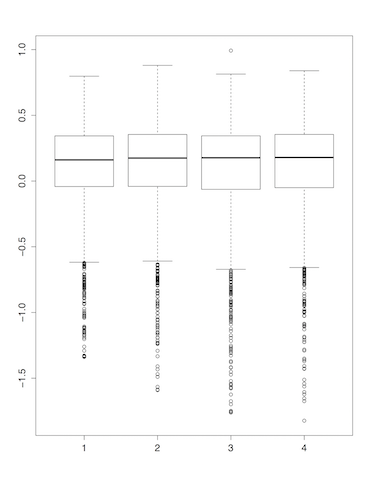
On remarque une stabilisation de la loi de $n^{-3/4}S_n$, toutes les boîtes à moustache semblant provenir de la même distribution. Ceci est conforme à (4), mais aussi au résultat de Gouëzel [3] qui montre la convergence en loi (sous $\nu_{3/4}$) de $n^{-3/4}S_n$ vers une loi stable d'indice $3/4$ (notons qu'ici nous n'avons pas tiré $y$ selon la loi $\nu_{3/4}$ qui n'est pas explicite, mais le même résultat de convergence est vrai si $y$ est tiré suivant la mesure de Lebesgue).
Considérons à présent le cas $\gamma=3/4$ et $\alpha=0.9$, de sorte que la vitesse dans (4) vaut $n^{\alpha/\gamma -1}=n^{1/5}$. Ce cas est plus difficile à illustrer que le précédent. On estime $ n^{1/5}{\nu_{3/4}}\left (|S_n | \geq (0.2) n^{9/10}\right )$ par $n^{1/5} \# \{y: S_n(y)\geq (0.2) n^{9/10}\}$, pour $N=16000$ tirages de $y$ selon la loi uniforme sur [0, 0.05]. On effectue cette estimation pour $n$ allant de
500 à 10000, avec un pas de 500. Le graphe obtenu est présenté ci-dessous (Figure 3).
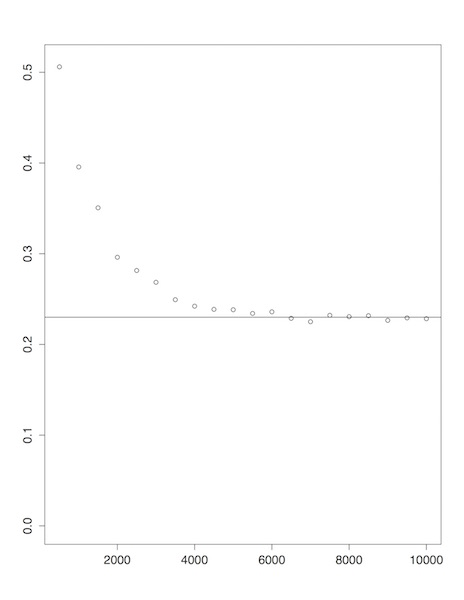
En trait plein, la droite d'ordonnée 0.23.
On observe quelque chose de plus précis que la limite supérieure prévue par (4), puisqu'il semble y avoir convergence vers une valeur non nulle (proche de 0.23).
Références
[1] J. Dedecker, S. Gouëzel and F. Merlevède, Some almost sure results for unbounded functions of intermittent maps and their associated Markov chains, Ann. Inst. Henri Poincaré Probab. Stat. 46 (2010) 796-821.
[2] J. Dedecker, S. Gouëzel and F. Merlevède, Large and moderate deviations for bounded functions of slowly mixing Markov chains, Stochastics and Dynamics 18 (2018) 38 pages.
[3] S. Gouëzel, Central limit theorem and stable laws for intermittent maps, Probab. Theory Related Fields 128 (2004) 82-122.
[4] C. Liverani, B. Saussol, and S. Vaienti, A probabilistic approach to intermittency, Ergodic Theory Dynam. Systems 19 (1999) 671—685.
[5] M. Rosenblatt (1956), A central limit theorem and a strong mixing condition, Proc. Nat. Acad. Sci. U. S. A. 42 43-47.
[6] L.-S. Young, Recurrence times and rates of mixing, Israel J. Math. 110 (1999) 153—188.
Contacts
Jérôme Dedecker est professeur à l’université Paris Descartes. Il est membre du laboratoire Mathématiques appliquées à Paris 5 (MAP5 - CNRS & Université Paris-Descartes).
Sébastien Gouëzel est directeur de recherche au CNRS. Il est membre du Laboratoire de mathématiques Jean Leray (LMJL - CNRS & Université de Nantes).
Florence Merlevède est professeur à l’Université Paris Est Marne-la-Vallée. Elle est membre du Laboratoire d’analyse et de mathématiques appliquées (LAMA - CNRS, Université Paris-Est Créteil Val-de-Marne & Université Paris-Est Marne-la-Vallée).