Les flux sanguins en équations et en images
Des collègues du laboratoire de mathématiques de Reims se sont intéressés à la simulation de la circulation des flux de liquides biologiques, notamment le sang dans les artères et les veines cérébrales.
Ce projet a impliqué une collaboration forte entre mathématiciens, informaticiens et physiciens ; il a réuni plusieurs équipes au niveau national dont le LMR, l’IRMA, le LJK, pour les mathématiques, ainsi qu’une entreprise innovante en logiciel libre pour l’imagerie médicale (Kitware SAS).
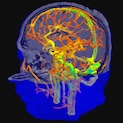
La formulation des équations qui régissent le mouvement du sang est un vieux problème que l’on peut faire remonter à Euler en 1775 et aux premiers travaux sur l’écoulement des fluides. Cependant, l’analyse du comportement des biofluides - tels que le sang dans nos vaisseaux sanguins - présente des caractéristiques propres. En effet, la particularité de ces fluides biologiques est qu’ils sont vivants ! Ils ne font pas que s’écouler, mais sont aussi en interaction avec leur milieu ; ils transportent des nutriments, de l’oxygène, ils ont une fonction biologique qui complique considérablement leur comportement.
La complexité des systèmes étudiés est telle que des hypothèses simplificatrices s’avèrent nécessaires. On suppose que le sang se comporte dans les grands vaisseaux comme l’eau, qui le compose principalement et on utilise donc les équations de la dynamique des fluides incompressibles dans un domaine, les équations de Navier-Stokes complétées par des conditions sur le bord du domaine. Par ailleurs, on fait abstraction des interactions fluide-structure, hypothèse notamment valide au niveau veineux. En effet, dans le cerveau, les vaisseaux sont enchâssés dans des structures méningées, et donc peu mobiles. Néanmoins, ce modèle n’est adéquat que dans la région intracrânienne, car au delà, les veines jugulaires, par exemple, se déforment en fonction de la vitesse du sang qui s’y écoule.
Dans l’article [1], les auteurs modélisent l’écoulement du sang dans le réseau veineux cérébral. Puis, ce modèle est appliqué à un réseau veineux cérébral réaliste - c’est-à-dire un maillage de calcul - obtenu à partir d’images IRM acquises sur des sujets volontaires (cf. Figure 1).
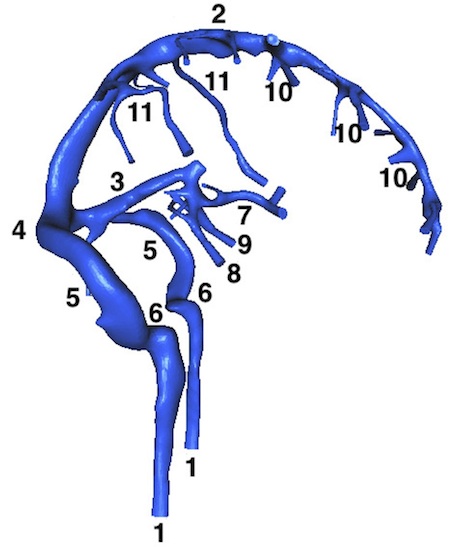
Un tel maillage de calcul est préalablement conçu grâce à des algorithmes de segmentation d’images spécifiquement adaptés aux réseaux tubulaires [2]. Ces algorithmes ont été mis au point, dans le cadre de ce projet, par Olivia Miraucourt et Odyssée Merveille, toutes deux lauréates de prix de thèse pour leurs travaux [3,4].
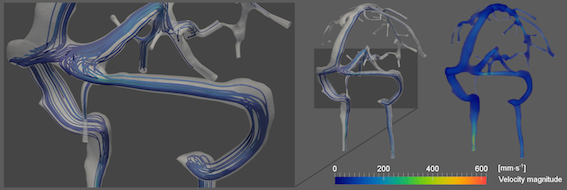
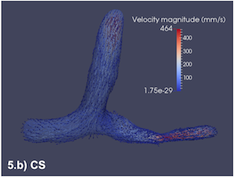
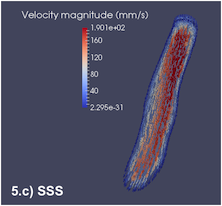
L’étude de la validité de ces simulations numériques des flux sanguins nécessite leur observation in vivo. L’unique moyen pour ce faire est d’avoir recours à des séquences spécifiques, notamment en imagerie par résonance magnétique (IRM). Il est alors envisageable de "comparer" des images réelles acquises en IRM avec les simulations. Mais, il faut alors pouvoir interpréter ces simulations de flux sanguins sous une forme équivalente, à savoir des données IRM simulées.
L’IRM permet d’observer les atomes d’hydrogène des molécules d’eau, via leurs propriétés magnétiques. En particulier, il est possible de quantifier leur mouvement par l’observation du déphasage de leur moment magnétique, proportionnel à leur vitesse. Les équations de Bloch, qui formalisent le mécanisme IRM, nous permettent alors de modéliser le lien phase-vitesse. La thèse d’Alexandre Fortin [5] a justement porté sur le développement d’une telle approche permettant de générer des images IRM à partir des simulations de flux sanguins.
Toutes ces méthodes ont été implantées sous forme de logiciels libres [6]. Ces outils permettent alors de mener des expérimentations visant à confronter les résultats de simulation obtenus avec des données réelles (fantômes physiques, données cliniques…).
Ces travaux permettent de progresser dans la compréhension du réseau vasculaire, dont les mécanismes sont encore largement méconnus à ce jour. Ils aident également à mieux corréler ce que l’on observe par le filtre de l’imagerie et les phénomènes qui se produisent réellement au sein des vaisseaux. Ils ouvrent de nombreuses perspectives, par exemple en termes d’enseignement de la médecine par des outils numériques, mais également pour la création d’outils de recherche reproductible pour l’analyse d’images.
Pour en savoir plus sur le projet VIVABRAIN, ANR-12-MONU-0010
Références
[1] O. Miraucourt, S. Salmon, M. Szopos et M. Thiriet. Blood flow in the cerebral venous system : Modeling and simulation. Computer Methods in Biomechanics and Biomedical Engineering, Vol 20, Issue 5, 2017, pp. 471 - 482.
[2] O. Merveille, O. Miraucourt, S. Salmon, N. Passat, H. Talbot. A variational model for thin structure segmentation based on a directional regularization. International Conference on Image Processing, pp. 4324 - 4328, 2016.
[3] O. Merveille. A morphological framework for curvilinear structure analysis. Application to the filtering and segmentation of blood vessels. Université Paris-Est, 2016. Prix de thèse AFRIF 2016.
[4] O. Miraucourt. Génération de modèles vasculaires cérébraux : segmentation de vaisseaux et simulation d’écoulements sanguins. Université de Reims Champagne-Ardenne, 2016. Prix de thèse "Numérique’" 2017 de l’Université de Champagne.
[5] A. Fortin. Simulation d’expériences d’angiographie cérébrale par résonance magnétique. Université de Reims Champagne-Ardenne, 2017. Lauréat de la finale régionale Champagne-Ardenne de MT180.
[6] N. Passat, S. Salmon, J. - P. Armspach, B. Naegel, C. Prud’homme, H. Talbot, A. Fortin, S. Garnotel, O. Merveille, O. Miraucourt, R. Tarabay, V. Chabannes, A. Dufour, A. Jezierska, O. Balédent, E. Durand, L. Najman, M. Szopos, A. Ancel, J. Baruthio, M. Delbany, S. Fall, G. Pagé, O. Génevaux, M. Ismail, P. Loureiro de Sousa, M. Thiriet, J. Jomier.From real MRA to virtual MRA : Towards an open-source framework, MICCAI, pp. 335 - 343, 2016.
Contact
Stéphanie Salmon est professeur à l'université de Reims-Champagne Ardenne. Elle est membre du laboratoire de mathématiques de Reims (LMR - CNRS & Université de Reims-Champagne Ardenne).