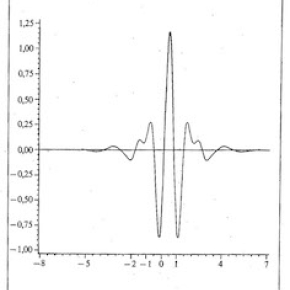
Les ondelettes à la base du mécanisme de détection des ondes gravitationnelles

On ne présente plus les décompositions en ondelettes. Issues de l’analyse de Fourier, elles sont l’héritage des intuitions des mathématiciens Haar et Gabor qui introduisirent, l’un, dès 1909, une fonction qui fut ensuite à la base de la théorie, et l’autre, en 1946, une décomposition temps-fréquence qui allait ensuite être généralisée. Baptisées ondelettes par Morlet et Grossman en 1984, ces fonctions sont utilisées pour transformer une fonction, quantité appartenant au domaine du continu, en un signal discret, une collection de nombres facilement stockables. Les ondelettes connurent en particulier un succès immense en imagerie puisqu’elles sont, par exemple, à la base du format JPEG 2000. La théorie mathématique des ondelettes fut réellement fondée par Yves Meyer dans les années 80 et ces années virent se développer une recherche intense autour des décompositions en bases d’ondelettes, qui ont une forme algorithmique particulièrement simple, puisqu’elles sont obtenues par des translations et dilatations d’une unique fonction, l’"ondelette mère" ; l’objectif étant à chaque fois d’augmenter et d’affiner leur caractère implémentable.

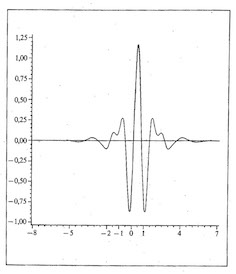
Les "bases de Wilson" ont une forme algorithmique un peu différente, puisqu’elle sont obtenues par des translations et modulations en fréquence d’une unique fonction. La décomposition sur une telle base fournit donc une analyse de Fourier à fenêtre. Leur existence avait été conjecturée par le physicien théoricien Wilson, et des exemples explicites de telles bases ont été construits par Daubechies, Jaffard et Journé en 1991. La fonction de base qu’ils utilisent présente l’avantage d’une localisation temps-fréquence remarquable : elle-même et sa transformée de Fourier ont toutes deux une décroissance exponentielle. Comme le disent les auteurs dans leur article publié en 1991 au SIAM Journal of Mathematical Analysis, "It is believed that such orthonormal bases could be useful in many contexts where lattices of modulated Gaussian functions are now used." Ce sont justement ces ondelettes que Necula, Klimenko et Mitselmakher proposent d’utiliser pour la détection des ondes gravitationnelles dans un article paru en 2012 au Journal of Physics. En effet, disent-ils, "the main advantages of the Wilson-Daubechies transform are the low computational cost, spectral leakage control, flexible structure of the frequency sub-bands, and the existence of the analytic time-delay filters, which are important for localization of the gravitational-wave sources in the sky."

Effectivement, c’est grâce à cette technique que l’on a pu détecter pour la première fois les ondes gravitationnelles.