Observabilité macroscopique des défauts de localisation dans la théorie de Boltzmann avec interactions à distance

Dans un travail récent, Cyril Imbert, Clément Mouhot et Luis Silvestre ont montré que les solutions de l'équation de Boltzman pour les interactions à longue portée, i.e. la densité de probabilité des particules en position et vitesse, ne pouvaient exhiber d'accumulation de particules aux grandes vitesses sans que les champs hydrodynamiques associés montrent également un comportement "pathologique", en l'occurrence une disparition ou concentration de la masse en un point d'espace, ou bien une concentration de l'énergie ou de l'entropie en un point d'espace.

L'équation dite de Boltzmann est en fait d'abord inventée par Maxwell en 1867 pour décrire la dynamique des gaz (à faible densité), dans un article fondateur de ce que l'on appelle aujourd'hui la mécanique statistique. Boltzmann a laissé son nom à cette équation du fait de la contribution majeure de son article de 1872 qui découvre la première formulation mathématique rigoureuse de l'entropie et du second principe de la thermodynamique pour les solutions mathématiques d'une équation. Pour les mathématiciens, l'équation de Boltzmann est une équation aux dérivées partielles (ÉDP), l'une des plus anciennes après les équations de la chaleur, de Euler et de Navier-Stokes ; elle est non-linéaire mais également "non-locale" du fait de termes intégraux.

Cette équation a pour fonction inconnue la densité de probabilité de présence des particules en position $x$ et vitesse $v$ au cours du temps $f=f(t,x,v) \ge 0$, et s'écrit en dimension $d \ge 2$
\begin{align*}
  & \partial_t f(t,x,v) + v \cdot \nabla_x f(t,x,v) \\
  & \qquad = \int_{R^d \times S^{d-1}}
  \left[ f(t,x,v') f(t,x,v'_*) - f(t,x,v) f(t,x,v_*) \right]
  B(v-v_*,\sigma) d v_* d \sigma.
\end{align*}
Le membre de gauche décrit le transport libre des particules lorsqu'elles n'interagissent pas, et le membre de droite décrit les interactions binaires $(v',v'_*) \to (v,v_*)$ (voir la figure 1) de manière statistique dans la limite de grande nombre de particules et faible densité, à travers l'opérateur de collision qui est une intégrale sur toutes ces interactions binaires possibles.

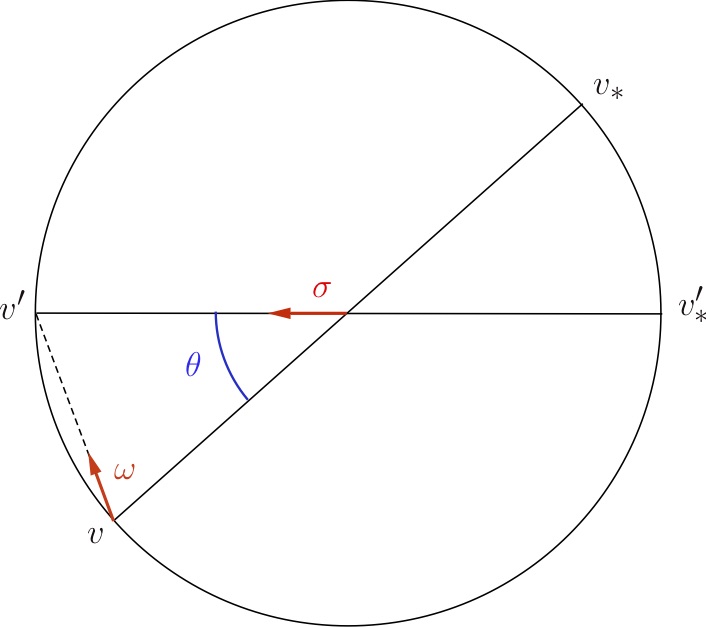
Dans celui-ci, le noyau de collision $B$ dépend du type d'interactions, et lorsque les particules sont chargées et interagissent à distance via les champs électromagnétiques, ce noyau est singulier pour les petites déviations, que l'on mesure à travers l'angle $\theta$ entre $(v'-v'_*)$ et $(v-v_*)$.

Cette équation est non-linéaire et non-locale et sa résolution reste aujourd'hui un défi fondamental pour les mathématiciens. On appelle "problème de Cauchy", en hommage à Cauchy et son théorème de Cauchy-Lipschitz pour les équations différentielles ordinaires, le problème de savoir si une équation différentielle, complétée par des conditions aux limites, admet une solution. Un tel problème est dit "bien posé" si la solution existe, est unique, et dépend continûment des données. Le problème de Cauchy, et son caractère bien posé ou non, dépendent de la topologie dans laquelle on cherche à construire des solutions. On ne sait pas aujourd'hui s'il existe un cadre "bien posé" pour le problème de Cauchy de l'équation de Boltzmann, en dehors de situations très symétriques ou proches de l'équilibre. La situation est en fait similaire aux équations de Navier-Stokes incompressibles en dimension trois, pour lesquelles le problème de construire des solutions régulières est l'un des fameux "problèmes du millénaire".

Face à cette difficulté, plusieurs physiciens mathématiciens suggèrent au tournant des années 1980 d'adopter un point de vue "a priori" (Muncaster, Truesdel, Cercignani), c'est-à-dire de supposer l'existence de solutions vérifiant certains propriétés minimales "vraisemblables" et d'essayer d'en déduire rigoureusement d'autres propriétés fondamentales de la théorie. Sous l'impulsion de Cercignani, Carlen, Toscani puis Villani et d'autres, cela a donné un programme de recherche sur le "retour à l'équilibre a priori", qui est maintenant complet dans le cas d'interaction de contact, et en passe de complétion dans le cas d'interaction à distance. L'objet de cet article concerne un autre programme de recherche qui s'en est inspiré et s'est développé plus récemment, impulsé par plusieurs articles de Luis Silvestre en particulier, sur la "régularité a priori".

Il est important pour la suite d'expliquer ici brièvement ce qu'était la découverte de Boltzmann. Maxwell avait remarqué que l'équation de (Maxwell)-Boltzmann admettait comme solutions stationnaires les répartitions gaussiennes en vitesse ; la théorie des probabilités et le théorème central limite n'était pas encore clarifiés à cette époque mais Maxwell faisait cependant déjà le lien avec les travaux sur la statistique des populations en Angleterre. Boltzmann "montre" ensuite que ces solutions stationnaires sont les seules autorisées, et que les solutions évoluent de manière irréversible vers ces équilibres stationnaires. Son argument repose sur la découverte de ce que l'on appellerait aujourd'hui une fonction de Lyapunov, mais que l'on nomme le plus souvent l'entropie de Boltzmann

\begin{equation*}
  \text{Entropie}[f(t,\cdot,\cdot)] := - \iint_{Domaine \times R^d}
  f(t,x,v) \ln f(t,x,v) d x d v.
\end{equation*}
Cette fonction est croissante au cours du temps. Cette découverte ne constitue pas pour autant une preuve mathématique car les solutions pour lesquelles justifier ce calcul ne sont pas construites. Insistons sur le fait que ce n'est pas un simple problème technique secondaire, car ce calcul repose sur certaines propriétés que doit avoir une solution, à commencer par le fait d'exister sur un intervalle de temps infini et de ne pas développer de singularités. Or ces propriétés pourraient se révéler fausses.

Néanmoins cette découverte fondamentale de Boltzmann guide les propriétés que l'on attend sur les solutions, en particulier le retour à l'équilibre et la "localisation" ou encore décroissance aux grandes vitesses. Ajoutons que suite à une longue série de travaux ouverte par les articles pionniers de Desvillettes dans les années 1990, on sait également que les interactions à distance produisent des effets de régularisation mathématiquement dus aux grands nombres de collisions rasantes, c'est-à-dire avec un angle de déviation petit. Dans les deux programmes de recherche a priori mentionnés précédemment, on travaille sur des solutions données "a priori" et dont les champs hydrodynamiques de masse, énergie et entropie sont contrôlés, c'est-à-dire que l'on suppose l'existence d'une solution classique $f(t,x,v)$ sur un intervalle de temps $[0,T]$ et qui vérifie : quel que soit

\begin{equation*}
  t \in [0,T], \ x \in {Domaine}, \quad
  \left\{
    \begin{array}{l}
      0 < m_0 \le \int_{R^d} f(t,x,v) d v \le M_0 < + \infty
      \\[3mm]
      \int_{R^d} f(t,x,v) |v|^2 d v \le E_0 \\[3mm]
      \int_{R^d} f(t,x,v) \ln f(t,x,v) d v \le H_0
    \end{array}
  \right.
\end{equation*}
pour des constantes $m_0,M_0,E_0,H_0 >0$, et l'on cherche à déduire les propriétés de retour à l'équilibre ou de régularité, si possible de manière optimale.

Dans l'article de Cyril Imbert, Clément Mouhot et Luis Silvestre, les données sont supposées périodiques en la variable d'espace, ce qui permet de travailler avec $x$ variant dans le tore plat $\mathbb T^d$ : c'est un cadre mathématique agréable qui permet d'éviter à la fois les questions de frontières et celles de fuite de particules à l'infini. Cependant, c'est une simplification qui devrait rapidement pouvoir être levée car par nature les hypothèses sur les champs hydrodynamiques ci-dessus et les résultats de régularité a priori sont locaux en espace. Nous démontrons alors que la solution $f(t,x,v)$ décroît polynômialement en vitesse, soit des estimations du type $f(t,x,v) \le C (1+|v|)^{-q}$ pour une constante $C>0$. Ce qui veut dire, en autres choses, qu'un défaut de localisation, et donc de thermalisation, sous la forme d'une "bosse glissante", soit un pic de concentration de particules se propageant vers les grandes vitesses, ne peut se produire, voir la figure 2 (une simplification sur cette figure est que ce défaut de localisation doit être mesuré avec les "moments ponctuels" $\sup_v f(t,x,v) |v|^q$).

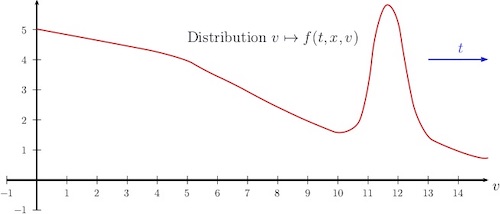
Remarquons qu'au vu du retour à l'équilibre attendu vers un équilibre avec décroissance gaussienne en vitesse, de telles estimations sont naturelles. Le résultat précis dépend du noyau de collision et pour l'expliquer il est nécessaire de présenter brièvement les différents noyaux de collisions.

Le noyau de collision provient de calculs sur la collision binaire $(v',v'_*) \to (v,v_*)$ en fonction de l'interaction supposée entre les particules, et de la statistique qui en résulte. L'équation de Boltzmann décrit la limite de grand nombre de particules et faible densité ; dans cette limite dite de "Boltzmann-Grad", le rayon des particules tend vers zéro, alors que la surface totale des particules reste d'ordre un. Les collisions binaires sont contraintes par les conservations de quantité de mouvement et énergie :
\[
  \left\{
    \begin{array}{l}
      v+v_*=v'+v'_*, \\[2mm]
      |v|^2+|v_*|^2=|v'|^2+|v'_*|^2.
    \end{array}
  \right.
\]
Les invariances par changement de repère impose que le noyau ne dépend que du module de la vitesse relative $|v-v_*|=|v'-v'_*|$ et de l'angle de déviation $\theta$ entre $(v-v_*)$ et $(v'-v'_*)$. Plus précisément pour les forces de contact (sphères rigides en collision élastique) il s'écrit $B=|v-v_*|$ et pour les interactions en puissances inverses il s'écrit $B=|v-v_*|^\gamma b(\cos \theta)$ pour un exposant $\gamma \in ]-d,1[$ et une fonction $b$ singulière en $\theta \sim 0$: $b \simeq \theta^{-d-1-2s}$ pour un $s \in ]0,1[$. Du point de vue mathématique, on peut faire une comparaison utile avec un opérateur différentiel en vitesse~: la dépendance en $|v-v_*|$ correspond à l'ordre de croissance des coefficients, et la singularité en $\theta \sim 0$ dicte l'ordre fractionnaire de différentiation (égal à $2s$). Notre résultat, de manière plus précise, énonce que, pour les interactions à distance en puissances inverses, la décroissance polynômiale $f(t,x,v) \le C (1+|v|)^{-q}$ apparaît à tout ordre $q$ lorsque $\gamma >0$, qu'elle est propagée dès lors qu'elle est vraie initialement pour tous les $\gamma$. Ajoutons également que nous montrons, de manière surprenante et encore un peu mystérieuse, une apparition de décroissance polynômiale d'ordre bas $-d-1-d\gamma/2s$ pour $\gamma \in ]-2s,2-2s]$ qui n'était pas attendue.

La démonstration repose sur deux ingrédients essentiels. Le premier est la mise en place d'un argument de "barrière" avec une fonction de barrière adaptée, ici $g(t,v) = N(t) (1+|v|)^{-q}$ pour une fonction $N(t)$ à ajuster qui explose éventuellement de manière polynômiale en $t=0$. Le but est alors de montrer que

\begin{align*}
 f(t,x,v) \le g(t,v) := N(t) (1+|v|)^{-q}
\end{align*}
en raisonnant par contradiction. On considère le premier point de contact éventuel $(t_0,x_0,v_0)$ entre les deux fonctions et l'on obtient en ce point les relations suivantes,
\begin{align*}
  \nabla_x f(t_0,x_0,v_0) =0, \quad \partial_t g(t_0,x_0,v_0) \le
  \partial_t f(t_0,x_0,v_0) = Q(f,f)(t_0,x_0,v_0),
\end{align*}
ainsi que $f(t_0,x_0,v) \le g(t_0,x_0,v)$ pour les autres vitesses $v \in R^d$. Le deuxième ingrédient de la preuve est alors de montrer que les collisions binaires "raréfient" les particules aux grandes vitesses, en moyenne. Autrement dit, il s'agit de montrer que l'opérateur $Q(f,f)$ calculé en $(t_0,x_0,v_0)$ est suffisamment négatif aux grandes vitesses. On part de la décomposition de $Q$ inspirée de la représentation dite de Carleman (1932), généralisée en un certain sens au cas d'interactions à distance par Alexandre, Desvillettes, Villani et Wennberg (2000) pour donner

\begin{align*}
  Q = Q_{singulier} + Q_{non-singulier},
\end{align*}
et on décompose ensuite de manière supplémentaire la partie singulière en suivant une idée venant de travaux de Silvestre sur le "cône de non-dégénerescence", et qui utilise également la représentation de Carleman, soit la paramétrisation de la collision par $v'_* \in R^d$ et $v' \in v + (v-v'_*)^\bot$, pour identifier des zones de coercivité. Cela aboutit à
\begin{align*}
  Q = Q_{singulier-favorable} +
  Q_{singulier-défavorable} +
  Q_{non-singulier}
\end{align*}
où la partie singulière "défavorable" est traitée comme un terme d'erreur aux grandes vitesses, alors que nous montrons des inégalités de coercivité sur la partie singulière "favorable".

Cet article est une étape dans l'étude de la régularité a priori. Les autres étapes sont établies dans des articles du premier et troisième auteur et permettent de résoudre la conjecture dans le cas de potentiels dits "modérément mous", c'est-à-dire lorsque la singularité en $\theta$ n'est pas trop forte (noyau de collision $B$ pour les interactions en puissance inverse ci-dessus avec $\gamma+2s \in [0,2]$). Des idées nouvelles seront nécessaires pour traiter le cas très singulier.