-A +A
Imprimer

Regards sur les ondes de matière observées dans les condensats de Bose-Einstein

Actualités scientifiques

Deux exemples de mise en œuvre de méthodes numériques dans le cadre de l’étude de la condensation de Bose-Einstein.

Un condensat de Bose-Einstein est un état de la matière aux propriétés très spécifiques : dans un gaz d’atomes identiques et sans interaction, à très basse température, une fraction importante du gaz s’accumule (ou condense) dans l’état quantique d’énergie minimale. Ouvrant de grandes possibilités d’applications, ce phénomène avait été conjecturé par Einstein en 1925, suite aux travaux de Bose. Néanmoins, il a fallu attendre 70 ans pour que soit produit et observé le premier condensat en 1995, ce qui a valu aux auteurs de cette réalisation le prix Nobel de physique en 2001. La modélisation des phénomènes apparaissant lors de cette condensation ouvre la voie à des réalisations numériques. Les deux images ci-dessous sont issues des travaux d’Ionut Danaila et de ses différents collaborateurs.

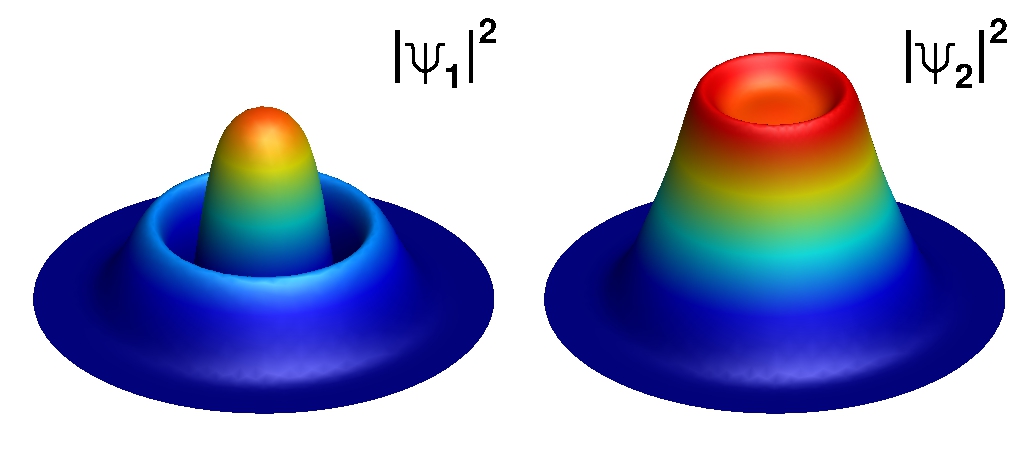
figure 1
Figure 1 : Grâce à un système numérique basé sur une méthode d’éléments finis adaptatifs, et en collaboration avec une équipe américaine, formée par le mathématicien P. Kevrekidis (University of Massachusetts Amherst) et les physiciens M. A. Khamehchi, V. Gokhroo et P. Engels (Washington State University), Ionut Danaila a pu explorer les ondes de matière observées dans les condensats de Bose-Einstein à deux composantes. Dans l’article [1], de nouveaux types d’ondes solitaires (ou soliton), qui généralisent la notion classiques de soliton noir (ou soliton trou, en anglais dark soliton), sont étudiés et simulés numériquement. Rappelons que la théorie des solitons a beaucoup d’applications en optique, acoustique, physique de la matière condensée, mécanique des fluides, etc. La figure 1 montre l’apparition d’une onde solitaire annulaire (dark-ring soliton) dans la première composante du condensat, contrecarrée par une onde solitaire de type anti-dark dans la deuxième composante.
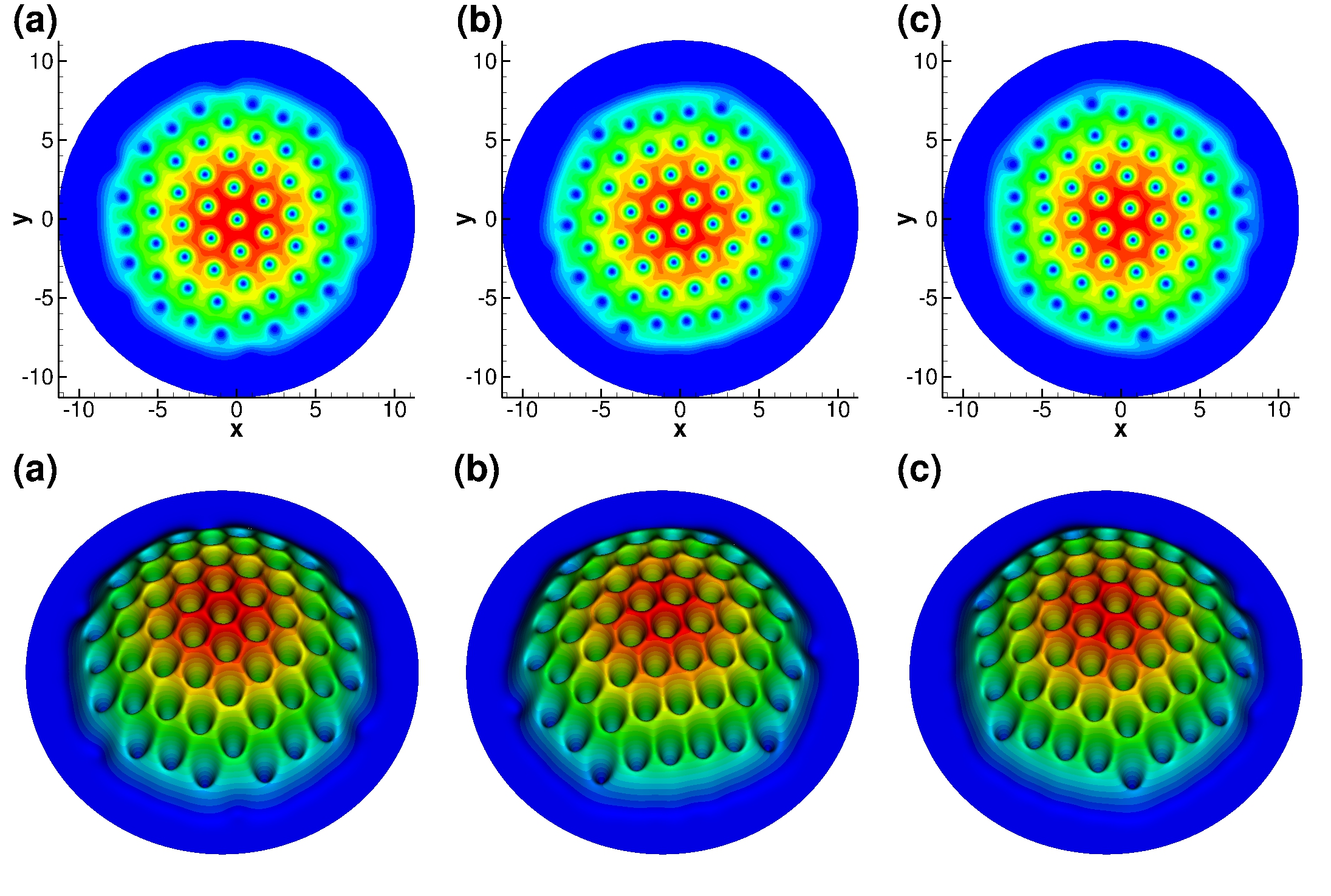
figure 2
Figure 2 : En combinant des concepts d’optimisation Riemanienne et la théorie des gradients de Sobolev, Ionut Danaila et Bartosz Protas (McMaster University) ont développé une méthode de gradient conjugué qui permet de calculer des configurations de vortex typiques des condensats de Bose-Einstein en rotation. La figure 2 ci-dessus met en lumière la répartition suivant un réseau hexagonal (réseau d’Abrikosov) d’un condensat de Bose-Einstein en rotation rapide.

 

Références

[1] I. Danaila, P. Kevrekidis, M. A. Khamehchi, V. Gokhroo et P. Engels, Vector dark-antidark solitary waves in multicomponent Bose-Einstein Condensates, Physical Review A, Vol 94, 2016.
[2] Ionut Danaila et B. Protas, Computation of Ground States of the Gross-Pitaevskii Functional via Riemannian Optimization (https://arxiv.org/pdf/1703.07693.pdf)

Contact

Ionut Danaila est professeur à l'université de Rouen Normandie. Il est membre du laboratoire de mathématique Raphaël Salem (LMRS - CNRS & Université de Rouen Normandie).