Représentations de groupes finis : de 0 à p

Les représentations linéaires des groupes finis ont tendance à se "décomposer" lorsque l’on passe d’un corps de caractéristique zéro à un corps de caractéristique positive $p$. La matrice de décomposition encode ce phénomène pour les représentations irréductibles. Dans le cas des groupes $\mathsf{GL}_n(q)$, $\mathsf{SO}_n(q)$ ou plus généralement des groupes réductifs sur un corps fini, cette matrice a une forme triangulaire. En d’autres termes, le passage de la caractéristique 0 à la caractéristique $p$ se fait sous la forme d’un système échelonné.

1- Représentations linéaires

Une représentation linéaire d'un groupe fini $G$ est un espace vectoriel, de dimension finie, muni d'une action linéaire de $G$. Par exemple, le groupe symétrique $\mathfrak{S}_n$ agit naturellement sur l'espace vectoriel $\mathbb{C}^n$ par $\sigma \cdot (x_1,x_2,\ldots,x_n) = (x_{\sigma(1)},x_{\sigma(2)},\ldots,x_{\sigma(n)})$ pour toute permutation $\sigma \in \mathfrak{S}_n$. En outre, cette action stabilise l'hyperplan donné par

$$ H = \{(x_1,x_2,\ldots,x_n) \in \mathbb{C}^n \, \mid \, x_1 +x_2 + \cdots + x_n = 0\}$$

ce qui montre que $H$ est aussi une représentation de $\mathfrak{S}_n$, mais plus petite. Elle ne contient d'ailleurs pas d'autre sous-espace vectoriel propre globalement stable par $\mathfrak{S}_n$, et à ce titre elle est dite irréductible.

Parmi toutes les représentations d'un groupe $G$, les représentations irréductibles sont particulièrement intéressantes puisqu'elles sont en quelque sorte les atomes de la théorie. Par exemple toute représentation complexe peut se décomposer en une somme directe de représentations irréductibles. En reprenant l'exemple précédent on trouve
$$\mathbb{C}^n  = H \oplus \mathbb{C}(1,1,\ldots,1).$$
Ici le groupe $\mathfrak{S}_n$ agit trivialement sur la droite portée par le vecteur $(1,1,\ldots,1)$, et on dit que la représentation associée est la représentation triviale.

Si l'on peut facilement connaître le nombre de représentations irréductibles d'un groupe fini (lorsque l'on travaille sur un corps algébriquement clos), il est en revanche difficile de les construire ou même de déterminer certaines de leurs propriétés basiques, comme leur dimension. On recherche souvent un paramétrage naturel des représentations irréductibles qui permet, entre autres :

• de calculer leur dimension ;
• de décomposer leur restriction à un sous-groupe ;
• de calculer leur caractère, à savoir la trace des éléments du groupe sur la représentation.

Ces problèmes ont été résolus pour de nombreux groupes "classiques" lorsque l'on travaille avec des représentations à coefficients dans $\mathbb{C}$ mais restent en général très ouverts en caractéristique $p>0$.

Pour le groupe symétrique $\mathfrak{S}_n$, il existe un paramétrage des représentations irréductibles complexes à l'aide des partitions de $n$, qui sont des suites décroissantes d'entiers positifs $\lambda = (\lambda_1\geq \lambda_2 \geq\cdots \geq \lambda_r \geq 0)$ vérifiant $\sum \lambda_i = n$. La représentation triviale correspond à la partition à un seul terme $(n)$ et la représentation donnée par $H$ construite plus haut correspond à la partition à deux termes $(n-1,1)$. On peut représenter graphiquement une partition par son diagramme de Young $\mathsf{Y}(\lambda)$; par exemple, la partition $\lambda = (4,2,1)$ de l'entier $7$ se représente par

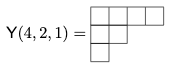
La dimension de la représentation irréductible $V_\lambda$ associée à la partition $\lambda$ se calcule à l'aide des crochets dans le diagramme de Young. Chaque boîte $b \in \mathsf{Y}(\lambda)$ dans le diagramme de $\lambda$ définit un crochet donné par l'ensemble des boîtes se situant à droite de $b$ et sur la même ligne ainsi que celles se situant en bas de $b$ et sur la même colonne, faisant de $b$ le coin supérieur gauche du crochet. En notant $\mathsf{h}(b)$ la taille du crochet, c'est-à-dire le nombre de boîtes qui le forment, on a \begin{equation*}\label{eq:hook}\tag{$\star$}
\mathsf{dim}\, V_\lambda = \frac{n!}{\prod_{b \in \mathsf{Y}(\lambda)} \mathsf{h}(b)}.
\end{equation*} En remplissant le diagramme précédent avec les tailles des crochets, on obtient

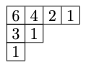
ce qui permet de calculer $$\mathsf{dim}\, V_{(4,2,1)} = \frac{7!}{6\cdot 4\cdot 2 \cdot 1 \cdot 3\cdot 1\cdot 1} = 35.$$ On retrouve aussi $\mathsf{dim}\, \mathbb{C} = \mathsf{dim}\, V_{(n)} = 1$ et $\mathsf{dim}\, H = \mathsf{dim}\, V_{(n-1,1)} = n-1$.
Remarquons que l'image d'un diagramme de Young par la symétrie par rapport à la diagonale est aussi un diagramme de Young. La partition associée est dite conjuguée, et on la note $\lambda^*$. On a bien sûr $\mathsf{dim}\, V_\lambda = \mathsf{dim}\, V_{\lambda^*}$. Par exemple, la partition conjuguée à $(n)$ est la partition $(1,1,\ldots,1)$. La représentation $V_{(1,1,\ldots,1)}$ associée est de dimension $1$ et définie par
$$ \sigma \cdot x = \mathsf{sgn}(\sigma)x$$
pour tout $x \in \mathbb{C}$ et $\sigma \in \mathfrak{S}_n$, où $\mathsf{sgn}(\sigma) = \pm 1$ est la signature de la permutation $\sigma$.

Précisons le cas $n=3$. Il y a trois partitions de l'entier $3$, à savoir $(3)$, $(2,1)$ et $(1,1,1)$, représentées par les diagrammes suivants :

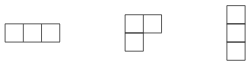
Les représentations associées sont respectivement la représentation triviale, celle de dimension $2$ donnée par le plan d'équation $x_1+x_2+x_3 = 0$ dans $\mathbb{C}^3$ et la représentation signature.

Changeons de groupe : considérons maintenant le groupe des matrices inversibles à coefficients dans le corps fini $\mathbb{F}_q$, que nous noterons $\mathsf{GL}_n(q)$. Il existe un paramétrage identique au précédent pour certaines représentations irréductibles de $\mathsf{GL}_n(q)$, dites unipotentes, dont les dimensions se calculent grâce à un $q$-analogue de la formule \eqref{eq:hook}. Si $\Delta_\lambda$ est la représentation unipotente associée à la partition $\lambda$ et si pour tout entier $i \geq 1$ on note $[i]_q = 1 + q + \cdots + q^{i-1}$, alors

$$\mathsf{dim}\, \Delta_\lambda = q^{\sum_i \lambda_i (i-1)\, } \frac{[n]_q [n-1]_q \cdots [2]_q [1]_q}{\prod_{b \in \mathsf{Y}(\lambda)} [\mathsf{h}(b)]_q}.$$

C'est un polynôme en $q$ dont la valeur en $q=1$ est la dimension de $V_\lambda$. Par exemple, pour les trois représentations unipotentes de $\mathsf{GL}_3(q)$, associées aux partitions $(3)$, $(2,1)$ et $(1,1,1)$, on obtient
$$ \mathsf{dim}\, \Delta_{(3)} = 1, \qquad  \mathsf{dim}\, \Delta_{(2,1)} = q(q+1), \qquad  \mathsf{dim}\, \Delta_{(1,1,1)} = q^3.$$

2 - Matrices de décomposition.

Dans la partie précédente nous avons beaucoup discuté des représentations irréductibles complexes. Que se passe-t-il lorsque l'on travaille sur un corps de caractéristique positive ? La construction est généralement plus ardue et les méthodes de la caractéristique zéro ne sont pas directement applicables.

Une façon naturelle d'aborder le problème est de considérer le passage de la caractéristique zéro à la caractéristique $p > 0$. En partant d'une représentation complexe irréductible, on peut chercher à la réduire modulo $p$ et voir quels composants irréductibles elle fait apparaître. Avant de donner plus de détails sur cette construction, reprenons l'exemple du plan d'équation $x_1 + x_2 +x_3 = 0$. Cette équation étant définie sur $\mathbb{Z}$, on peut la considérer sur n'importe quel corps, notamment sur le corps fini $\mathbb{F}_p$. On dispose donc de la représentation de dimension $2$ $$H = \{(x_1,x_2,x_3) \in \mathbb{F}_p^3 \, \mid \, x_1 + x_2 +x_3 = 0\}.$$ Est-elle toujours irréductible ? Si elle ne l'est pas, cela veut dire qu'elle contient un sous-espace de dimension $1$ stable par $\mathfrak{S}_3$, autrement dit qu'il existe un vecteur non nul de ce plan qui soit vecteur propre pour toutes les permutations. On peut se convaincre que cela n'arrive jamais, sauf dans le cas où $p=3$ ! Car alors le vecteur $(1,1,1)$ appartient au plan, et il est invariant par l'action de $\mathfrak{S}_3$. On ne peut pas lui trouver un supplémentaire stable, mais on peut tout de même considérer la suite exacte courte \begin{equation}\label{eq:ses} \tag{$\star\star$}
 0 \longrightarrow  \mathbb{F}_3 (1,1,1)  \longrightarrow H \longrightarrow  V \longrightarrow0
\end{equation} où $V = H/\mathbb{F}_3 (1,1,1) $ est l'espace vectoriel quotient, de dimension $1$, sur lequel $\mathfrak{S}_3$ agit aussi. Cette action se calcule : pour la permutation $\sigma = (1,2)$ on trouve $$\begin{aligned} \sigma \cdot (x_1,x_2,x_3) + (x_1,x_2,x_3) & \, = (x_1+x_2,x_1+x_2,x_1+x_2) \\
& \, = (x_1+x_2)  (1,1,1) \\\end{aligned} $$
car $2x_3 = -x_3 = x_1+x_2$. On en déduit que la représentation $V$ n'est autre que la signature, en caractéristique $3$. Cela montre que la représentation complexe de dimension $2$ peut s'écrire, en caractéristique $3$, à l'aide des deux représentations irréductibles de dimension $1$. Ce sont donc les seules en caractéristique $3$.

Plus généralement, étant donnée une représentation irréductible complexe de $G$, on peut, en fixant un isomorphisme de corps $\mathbb{C} \simeq \overline{\mathbb{Q}}_p$, en trouver un modèle sur une extension finie de $\mathbb{Z}_p$, que l'on peut ensuite réduire modulo $p$ pour obtenir une représentation de $G$ sur un corps fini de caractéristique $p$. Cette représentation dépend du choix du modèle entier, mais pas les représentations irréductibles qui la composent. La matrice de $p$-décomposition encode, pour chaque représentation irréductible complexe de $G$, les représentations irréductibles sur $\overline{\mathbb{F}}_p$ qui apparaissent dans la réduction modulo $p$, avec leur multiplicités. A l'aide de la suite exacte \eqref{eq:ses}, l'exemple du groupe symétrique $\mathfrak{S}_3$ en caractéristique $3$ donne la matrice suivante $$\begin{array}{c} V_{(3)} \\ V_{(2,1)} \\ V_{(1,1,1)} \end{array} \left[ \begin{array}{cc} 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{array} \right] $$ dont les lignes sont indexées par les représentations irréductibles complexes, et les colonnes par les représentations irréductibles à coefficients dans $\overline{\mathbb{F}}_3$.

Pour le groupe symétrique $\mathfrak{S}_3$, un autre cas est intéressant, celui de $p=2$. Cette fois-ci la représentation donnée par l'hyperplan d'équation $x_1+x_2+x_3 = 0$ est irréductible ; en revanche, puisque $1 = -1$ dans le corps $\mathbb{F}_2$, on ne peut pas distinguer la représentation triviale de la représentation signature dans ce cas. La matrice de décomposition est alors donnée par
$$\begin{array}{c} V_{(3)} \\ V_{(2,1)} \\ V_{(1,1,1)} \end{array} \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 1 & 0 \end{array} \right]. $$  
Les cas $p=2$ et $p=3$ sont pour ainsi dire les seuls cas intéressants en caractéristique positive pour le groupe symétrique $\mathfrak{S}_3$. Plus généralement, si $p$ ne divise pas l'ordre du groupe fini $G$, rien ne change lorsque l'on passe des coefficients complexes aux coefficients dans $\overline{\mathbb{F}}_p$. Autrement dit la matrice de décomposition est la matrice identité dans ce cas.

S'il est aisé de calculer les matrices de décomposition de petits groupes, ce calcul s'avère complètement inaccessible pour la plupart des groupes. Même en utilisant des programmes informatiques permettant de travailler avec des représentations explicites, on ne connaît les matrices de décomposition de $\mathfrak{S}_n$ que pour $n$ relativement petit. Beaucoup de travaux autour de ces matrices se concentrent sur le calcul de certaines entrées ou leurs valeurs approchées ainsi que sur la forme générale de la matrice (triangularité, disposition des entrées nulles...).

Nous avons vu que certaines représentations complexes de $\mathsf{GL}_n(q)$ se comportaient comme des $q$-analogues des représentations de $\mathfrak{S}_n$. En caractéristique $p$ la situation est un peu moins claire. Par exemple, si $p > 3$, on trouve les matrices de décomposition suivantes pour les représentations unipotentes de $\mathsf{GL}_3(q)$ :
$$\begin{array}{c@{}c@{ \qquad}c@{\qquad}c} \begin{array}{c} \Delta_{(3)} \\ \Delta_{(2,1)} \\ \Delta_{(1,1,1)} \end{array} & \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] &
\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right] & \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right] \\
 & {}_{p \mid q-1} & {}_{p \mid q+1} & {}_{p \mid q^2 +q +1} \\ \end{array}
 $$  
Ici, nous avons distingué les cas selon le facteur cyclotomique que $p$ divise, et omis le cas $p \mid q$. Rappelons en effet que l'ordre du groupe $\mathsf{GL}_3(q)$ vaut
$$|\mathsf{GL}_3(q)| = (q^3-1)(q^3-q)(q^3-q^2) = q^3(q-1)^3(q+1)(q^2+q+1).$$
Sur cet exemple on peut observer les propriétés suivantes de la matrice de décomposition :

• la matrice est carrée ;
• les coefficients de la matrice ne dépendent pas de $q$, mais seulement de l'ordre de $q$ dans $\mathbb{F}_p^\times$. Il n'y a donc qu'un nombre fini de matrices de décompositions lorsque l'on fixe le groupe mais que l'on fait varier $p$ et $q$ ;
• la matrice a une forme unitriangulaire.

Ces trois propriétés sont connues pour $\mathsf{GL}_n(q)$ depuis les années 80. Lorsque l'on travaille avec d'autres groupes réductifs sur des corps finis, comme $\mathsf{SO}_n(q)$ ou $\mathsf{Sp}_{2n}(q)$, la première propriété a été démontrée par Geck-Hiss au début des années 90 \cite{GH}, mais les autres résistent depuis de nombreuses années. Dans un travail en récent [2], nous avons réussi à montrer la dernière.

Théorème. Soit $\mathbf{G}$ un groupe réductif connexe défini sur $\mathbb{F}_q$ et $G := \mathbf{G}(\mathbb{F}_q)$ le groupe fini de ses points rationnels. Si $p$ et la caractéristique de $\mathbb{F}_q$ ne sont pas trop "petits'', la matrice de décomposition des représentations unipotentes de $G$ a une forme unitriangulaire.

Que gagne-t-on à disposer d'une propriété d'unitriangularité ? On peut en quelque sorte construire pas-à-pas les représentations modulaires à coefficients dans $\overline{\mathbb{F}}_p$) à partir des représentations complexes. La première ligne de la matrice nous dit juste que la représentation triviale sur $\mathbb{C}$ donne la représentation triviale sur $\overline{\mathbb{F}}_p$. La seconde ligne nous dit qu'en réduisant une représentation complexe bien identifiée, on obtient plusieurs copies de la représentation triviale plus une copie d'une nouvelle représentation modulaire, jusqu'ici inconnue. En continuant ainsi on peut déterminer les représentations modulaires et même calculer leur dimension si l'on connaît explicitement la matrice de décomposition.

L'unitriangularité nous donne une bijection canonique entre les représentations unipotentes complexes et modulaires. Cela peut être utile pour étudier l'action des automorphismes de $G$ sur les représentations modulaires à partir de l'action sur les représentations complexes, en général plus facile à déterminer.

Il existe des groupes finis pour lesquels les matrices de décomposition ne sont pas unitriangulaires. Le fait que ce soit le cas pour les groupes réductifs sur les corps finis n'est pas fortuit, et il est conjecturé que cette propriété "numérique" est le reflet d'une propriété structurelle de ces groupes et de la géométrie des groupes algébriques sous-jacents. Des outils très élaborés (équivalences dérivées perverses) ont été mis au point pour expliquer ces phénomènes, en lien avec la conjecture du défaut abélien de Broué [1].