Transport optimal de sable avec une pelle et un seau, nouveaux outils pour l'analyse statistique de données ?

L'Analyse en Composantes Principales (ACP) est un outil privilégié en statistique pour la réduction de dimension et la visualisation des variations d'un ensemble de données autour de leur moyenne. Toutefois, lorsque les observations peuvent se modéliser comme des densités de probabilités (ou plus généralement des mesures), l'ACP usuelle n'est pas nécessairement adaptée. Dans ce contexte, il peut être alors intéressant d'utiliser la notion d'ACP le long de géodésiques dans l'espace des mesures de probabilités muni de la distance de Wasserstein [2, 3, 6]. Les progrès récents [4] sur les aspects numériques de la résolution de problèmes d'optimisation issus de la théorie du transport optimal [1, 7] permettent à présent d'envisager l'utilisation de ce type d'ACP pour l'analyse statistique de données. Le problème de l'optimisation d'un coût de transport (par exemple d'un tas de sable vers un trou à l'aide d'une pelle et d'un seau) tel que formulé par Gaspard Monge au 18ème siècle conduit donc, depuis récemment, à de nouvelles techniques numériques pour le statisticien.

Une problématique classique de la statistique est de pouvoir visualiser les variations principales d'un ensemble de données autour de leur moyenne. L'Analyse en Composantes Principales (ACP) est un outil privilégié pour répondre à cette question qui revient à la diagonalisation de la matrice de covariance des données. Afin d'illustrer le principe de l'ACP, on peut considérer l'exemple du nuage de points dans le plan (données bi-dimensionnelles) de la Figure 1(a). La moyenne usuelle de ces données est le point en rouge qui le centre de ce nuage de points (barycentre Euclidien). L'ACP de ces données conduit à construire deux droites orthogonales qui représentent la première et la deuxième direction principale de variation de ce nuage de points autour de sa moyenne (voir Figure 1(b)).

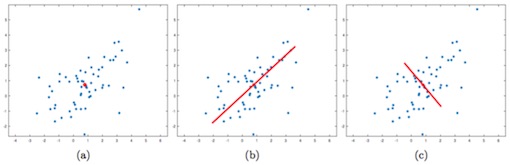
Implicitement, l'ACP usuelle revient à considérer que les données peuvent se modéliser comme des éléments d'un espace Euclidien (ou de Hilbert). Toutefois, lorsque les données peuvent se représenter sous la forme de densités de probabilités (ou plus généralement de mesures de probabilités) cette approche peut présenter quelques limitations.

A titre d'illustration, il est présenté dans la Figure 2 un exemple d'ACP d'un ensemble de densités gaussiennes dont les moyennes et variances sont aléatoires (et indépendantes).

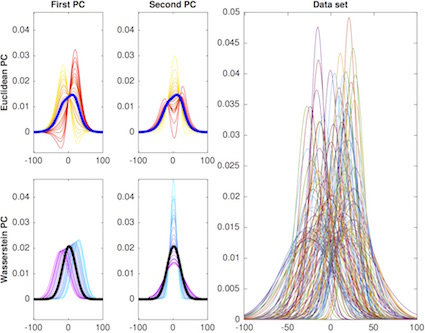
Les limites d'une ACP euclidienne sur cet exemple sont alors les suivantes :

• la moyenne des données n'est pas une gaussienne,
• les directions principales de variations (qui sont ici des géodésiques dans l'espace de Hilbert des fonctions de carré intégrable qui passent par la moyenne) se font le long de courbes qui ne sont pas des densités de probabilités car celles-ci prennent des valeurs négatives et ne sont pas d'intégrale égale à un.

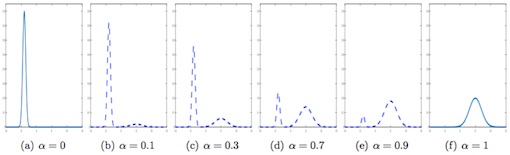
Les limitations d'une telle ACP peuvent également s'expliquer à partir de l'exemple de la Figure 3 qui représente la géodésique entre deux densités gaussiennes lorsque celles-ci sont modélisées comme des éléments d'un espace de Hilbert.

Une alternative possible pour des données sous la forme de densités de probabilités est de les considérer comme des mesures de probabilités appartenant à l'espace de Wasserstein, et d'utiliser les outils issus du transport optimal pour analyser leurs variations le long de géodésiques dans cet espace. Le transport optimal est un problème ancien qui a connu récemment un formidable développement à la fois du point de vue mathématique [7] et numérique [4] pour des applications à un panel très large de problèmes d'analyse de données en traitement d'images, apprentissage statistique et intelligence artificielle.

L'intérêt de l'utilisation du transport optimal pour modéliser les variations d'un ensemble de densités de probabilités est illustré dans la Figure 4 qui présente un exemple d'une géodésique dans l'espace de Wasserstein entre deux mesures gaussiennes.

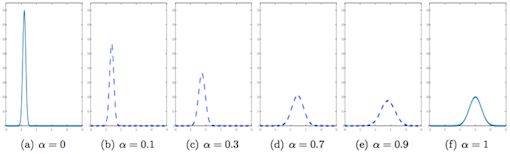
Dans ce cas, la structure des données est bien préservée le long de la géodésique qui reste une séquence de mesures gaussiennes. Ceci n'est pas le cas avec une modélisation plus classique de densités comme des éléments appartenant à un espace de Hilbert comme l'atteste l'exemple de la Figure 3.

Récemment, il a été proposé dans [2, 3, 6] de s'intéresser à la définition d'une notion d'ACP le long de géodésiques principales pour des mesures de probabilités aléatoires dans l'espace de Wasserstein. Cette formulation implique la résolution numérique de problèmes d'optimisation non-triviaux liés à une ACP dans des espaces non-linéaires qui peuvent se résoudre grâce à la structure géométrique pseudo-riemannienne des espaces de Wasserstein, ainsi qu'au travail fondateur d'Agueh et Carlier [1] sur la notion de barycentres de Wasserstein.  

Nous présentons ici deux exemples de ce type d'ACP :
- d'une part pour des densités de probabilités à support sur la droite réelle (voir Figure 3) qui sont des données simulées,
-  d'autre part  pour des images réelles bi-dimensionnelles dont les valeurs des pixels ont été normalisées afin de pouvoir les considérer comme des densités de probabilités (voir Figure 5).

Au vu de la Figure 3, l'ACP géodésique dans l'espace de Wasserstein permet de mieux mettre en évidence que les deux principales sources de variations dans les données sont une translation (changement de moyenne) et une dilatation/rétraction (changement de variance) de la densité gaussienne standard qui est ici le barycentre de Wasserstein de ces données. Il apparaît également l'intérêt de cette approche par rapport à une ACP standard.

L'analyse de la base de données MNIST [5] par ACP géodésique qui est proposée dans la Figure 5 permet de mieux prendre en compte les sources de variabilité de la forme géométrique des chiffres manuscrits par rapport à une ACP standard. Pour l'ensemble des chiffres, il apparaît une source de variabilité en rotation autour de leur barycentre ainsi qu'un effet de rétraction ou dilatation. Pour le chiffre 2, l'ACP au sens du transport optimal permet également de mettre en évidence une variation de son écriture sans puis avec une boucle le long de la première géodésique principale.

Les applications potentielles du transport optimal pour l'analyse de données sont de plus en plus nombreuses. Pour une série d'exemples illustratifs et de codes en ligne, on pourra consulter le livre récent de Cuturi et Peyré [4]. Ces outils permettent également de proposer aux statisticiens de nouvelles méthodologies d'analyse de données pour lesquelles l'utilisation des propriétés géométriques du transport optimal est pertinent.