Les nombres quantiques ? Surely you’re joking, Mr. Feynman !
Les idées de la physique quantique ont eu un impact énorme sur le développement des mathématiques, tous ses domaines ont été influencés. Nombreuses notions ont émergé, comme entre autres, les groupes et algèbres quantiques, le quantum calculus, les fonctions spéciales. Les nombres, concept le plus élémentaire et ancien au coeur de mathématiques depuis les babyloniens, devraient eux aussi avoir leur place dans le paysage quantique. Dans deux articles récents, Sophie Morier-Genoud, professeure à l'Université de Reims Champagne Ardennes et Valentin Ovsienko, directeur de recherche au CNRS, tous deux membres du Laboratoire de Mahématiques de Reims1 , ont introduit une notion de nombres réels quantiques, ou «q-nombres». Ce travail a suscité l’intérêt de beaucoup de chercheuses et chercheurs et vient d’être récompensé par le prix David Robbins 2025 de l’American Mathematical Society.
- 1UMR9008 - CNRS/Université de Reims Champagne-Ardennes
Le point de départ du nouveau concept de q-nombres n’est pourtant pas basé sur les travaux de Max Planck ou Albert Einstein, mais plutôt sur ceux d’Euler et Gauss. Bien avant l’ère quantique, les travaux de ces deux titans ont permis l’émergence de q-nombres entiers, une théorie qui se trouve à l’interface de la combinatoire et arithmétique. Les célèbres coefficients q-binomiaux sont les vedettes de cette théorie. Ce sont des polynômes d’une variable (notée q par tradition). Le rôle des coefficients q-binomiaux en mathématique est immense, mais ils sont également utilisés par les physiciens théoriciens. En physique, le paramètre q est égale à eh, où h=6.62607015x10-34 (joules par seconde) est la constante de Planck. Incapables de retenir la valeur exacte de h et attirées par l’abstraction, les mathématiciennes et mathématiciens préfèrent parler de h comme un «paramètre infinitésimalement petit ». On ne déduit absolument pas de la petitesse de h que son exponentielle q est proche de 1 ! En mathématique, le paramètre q peut prendre toutes les valeurs surréalistes selon les approches et théories. Il peut être réel, ou au contraire racine de -1, ou bien un paramètre formel, il peut aussi être une puissance d’un nombre entier premier.
Les q-rationnels ont une grande ressemblance avec les coefficients q-binomiaux. Pour les définir, il suffit de remplacer dans la définition des q-binomiaux le triangle de Pascal par un arbre binaire ; l’arbre de Farey. Mais il y a aussi une grande différence : les q-rationnels sont des fonctions rationnelles en q. Une autre différence est le groupe de symétrie, cette notion, fondamentale en mathématique qui suffit elle-même parfois pour définir tous les objets. Le groupe de symétrie des q-nombres est le célèbre groupe modulaire, qui joue par ailleurs un rôle central dans la théorie des nombres moderne. Un aspect agréable et attirant des q-rationnels est leur simplicité, ils sont faciles à définir et à manipuler.
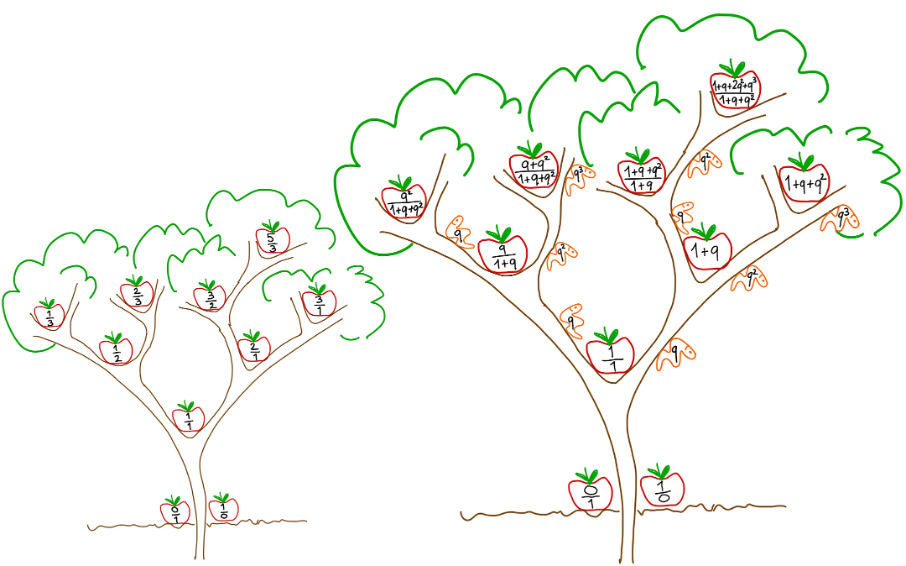
Les q-irrationnels s’obtiennent des q-rationnels par convergence des séries de Taylor. Ce sont des séries en q à coefficients entiers et leurs propriétés ne sont pas encore toutes connues. Par exemple, l’interprétation des coefficients des q-irrationnels reste une énigme, notamment les coefficients de la série qui représente le nombre π.
La beauté des mathématiques est due entre autre à la polyvalence synthétique de ses notions : les mêmes formules apparaissent dans des sujets différents pour décrire des phénomènes non liés de prime abord. Nos protagonistes, les coefficients q-binomiaux, servent en combinatoire pour énumérer des objets, en géométrie pour compter des points sur les corps finis, en physique mathématique pour décrire le plan quantique. Cette universalité, difficile à expliquer, semble être partagée par les q-nombres. Des propriétés remarquables qui relient les q-rationnels à la géométrie, combinatoire et analyse ont été démontrées ou observées par des expériences numériques dans plusieurs travaux. L’une de propriétés est l’unimodalité, le concept fondamental de mathématiques. Les premiers pas pour comprendre les propriétés analytiques des q-irrationnels ont été faits et donnent des applications à la théorie classique des groupes de tresses.
La théorie des q-nombres fait ses tout premiers pas, cette théorie reste à développer. Le défi le plus important est de comprendre le lien à la physique. Mais pour faire cela il faudrait d’abord savoir si Euler aurait préféré discuter avec Einstein et Gauss avec Planck, ou vice-versa… A moins que tous les quatre se soient réunis pour envoyer une foudre et bruler les q-nombres ?! Cette chimère avec le visage d’un bébé et la queue d’un monstre !
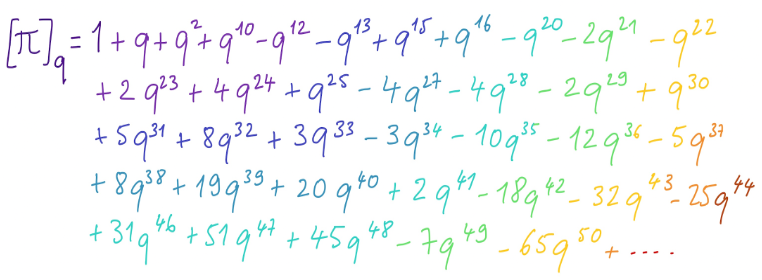
Références
S. Morier-Genoud, V. Ovsienko, q-deformed rationals and q-continued fractions. Forum Math. Sigma 8 (2020), 55 pp.
S. Morier-Genoud, V. Ovsienko, On q-deformed real numbers. Experimental. Math. 31 (2022).
