Maths & Musique #4 : The same second skin, by Thomas Menuet

After a two-year artistic residency at theInstitut de Recherche Mathématique de Rennes (IRMAR), Université de Rennes, I've learned a great deal through my contact with many researchers. In this article, I'd like to share a little of that wonderment with you, as a musician, by describing some of the realizations I consider important, some of which have had a lasting impact on my musical life.

It all begins on October 6, 2022. At 9 a.m., I am introduced to the administrative team on whom I can rely if need be. I'm invited at 10:15 a.m. to an unfamiliar seminar, followed by another at 1 p.m., this time on algebraic geometry. But before that I meet Michel Gros at 9.30am. Intrigued by the presence of a musician within the walls ofIRMAR, he wants to meet me and probe my knowledge a little. I ask a few naïve questions about what a mathematician's day is like. He's currently working on theobservability inequality using elliptic equations. We part politely after this first observation.

The two seminars follow on from the interview, and I don't understand a word of it. The same goes for the next two weeks. I start to question myself about what I'm doing here, about everything that's happening in front of me and that I'm missing out on so badly. Frustrated at not having any grip on reality, I decide to reflect on this by staying at home for the following week. Total imposture and shame take over my mind Am I legitimate here? Once again, even if it's what I'm really after, I'm in a situation that reduces me to nothing, and above all shows me the full extent of my powerlessness. However, I'll have to manage to capture this knowledge somehow, which for the moment is slipping through my fingers like fine sand. Then this difficult moment passes, as if I've finally accepted not that I'm legitimate, but that I need to acclimatize myself to something other than my daily life as a musician. Perhaps this acclimatization is the key. And it was here, almost in spite of myself, that things changed.

It was one of the most important realizations of those two years “ You don't really learn, you acclimatize to the context you're studying, and you understand ”. This is the daily life of mathematicians here, the very definition of research. To desire the truth, to confront it as much as the difficulty of understanding its context, which is necessary for it to blossom. In this world, bare and silent, wild and unadapted to what we are, we must succeed in extending our vision beyond our inconsistency, and this is an effort, a real one, because before the obvious, we see almost nothing. So, since it's only once we've located the zone of truth through intuition that we'll be able to inhabit its context, we'll be obliged by its rules to develop the muscularity necessary to understand it, and more broadly, to understand what we think we know about what mathematics is. What is it anyway, infinity at all ends and in constant extension, no?

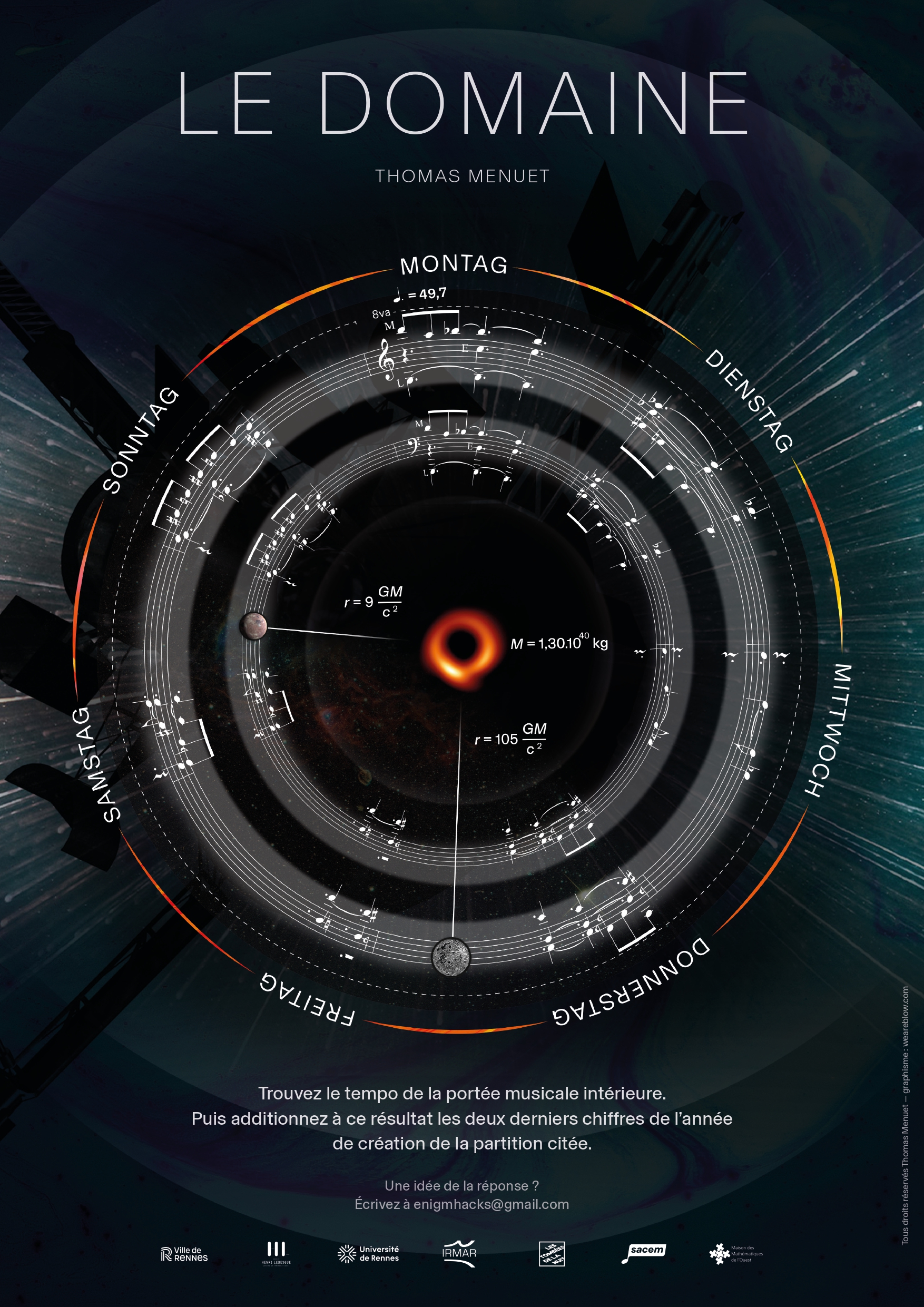Glow (Lueur) enigma (nuclear fusion)	The domaine enigma (space)

A coded language whose sole purpose is to make us aware of who we are and what surrounds us. You'd be forgiven for thinking that mathematics would exist without us. Of course, this is not the case. It reveals us, awakens us, thanks to us, like music.

It's the glove that adapts to each individual's hand through the power of our mind. It's a second skin for our being, which will always fit us at every moment of our lives, to explore the dark places that preoccupy us. Guided by our conscience, it will always be there to tell us that we did the right thing, that we were right within a well-defined framework. That, by dint of hard work, we always manage to get it right in the end. She is ourselves, our past and our present, a condensed lightning bolt that crosses the night all around us and, if we wish, inhabits us. It's our future too, with the constantly renewed truth as our compass, which we instinctively feel exists somewhere, without yet knowing where. And that's what researchers are all about.

It is never-ending, for each awakening is an arrival that is immediately transformed into a step towards another awakening. In other words, there is a correlation in this world between the desire to rediscover that feeling of insight and the new questions that this unveiling raises in its wake, new questions that will then be the breeding ground for the next awakening, and so on. To rediscover this feeling of awakening, it's important to know how to multiply our chances. And to do this, we need to multiply the angles of approach and understanding of our subject by being creative and unexpected, by exchanging with others. This is what mathematical researchers do.

How do you decipher a Caesar code in the French language without laboriously trying out every possible solution for shifting the letters? The answer lies in the frequency of the “e” in the French language. By locating the letter that replaces the “e”, you simplify the deciphering process. It's an original solution, both simple and elegant, effective and so gratifying to feel the clarity of the mechanism afterwards.

A similar question arose for me musically in the third work I'm creating for this residency, which deals with Mathematical Truth. Here are the four subjects you'll be able to hear musically from December 2024: the place of women in mathematics (Némésis), the passing of knowledge between generations (Héritage), truth (Vérité), and the construction of the mathematical mind (Esprit). But what is mathematical truth? No idea, of course... except perhaps for one thing: it's a contextual truth.

Cyber horizon enigma (quantum computer security)	Tribute (Hommage) enigma (telecommunication)

When a researcher tries to find an equation, his or her first reflex is to contextualize it, i.e. to place it in a set of numbers: ℕ, ℤ, 𝔻, ℚ, or ℝ. Each of these sets will not give the same result to the equation. Several solutions in ℝ, and perhaps none in ℕ. But then, where's the real solution? They're all true, I'm told, which means that depending on its context, an equation has several truths. Truth in mathematics is therefore contextual. So how do we convey this fact, and above all, make it best understood through music?

I used a well-known theme that I rewrote in different divisions of the octave, like the different realities of an equation in set theory. In 4, in 7, in 12 (½ piano tones), in 15 and finally in 24 notes. This of course leads to ¼ tones scattered here and there, but above all, it musically opens up new horizons, the famous questions leading us towards another awakening. Here are a few of them below:

What becomes of this theme, initially known in 12 semitones, with these new cuts? Is it a different one, or is it still the same? In other words, even if the notion of truth is not self-evident in art, the question of what is right forces us to ask whether, through the senses, we perceive the same or another theme? Do we perceive this theme as always being the same with 12 ½ tones, or is it perceived quite differently in contact with others? Where is the real theme? At 12 ½ tones, of course, but are we sure? Are we entitled here to impose on perception what we know to be true from reason (several contextual truths)? Is music any more true than mathematics? The variation of the theme through the modification of its context that this math/music analogy entails is, for me, entirely new to music. And this idea comes from mathematics.

Over and above these musical works and the questions they raise, and with the help of the cultural service of the University of Rennes, we worked on putting together 10 mathematical and musical riddles with contemporary graphics. These two projects are based on the idea that music and mathematics enable us to see far beyond our senses. By what miracle was it ever possible to project ourselves so far, to awaken us beyond ourselves, our bodies and time?

The 10 riddles are presented in the form of an exhibition, and the 4 musical works in the form of a concert. For further information, please contact Guillaume Julien, head of communications at Le diapason: guillaume.julien@univ-rennes1.fr