Des flippers de taille infinie

Le modèle du {gaz de Lorentz} a été introduit en 1905 par Lorentz [8]. Il modélise l’évolution de particules ponctuelles se déplaçant à vitesse unité de manière rectiligne entre des obstacles circulaires ou elliptiques (deux à deux disjoints) placés de manière $\mathbb Z^2$-périodique dans le plan et obéissant à la loi de la réflexion de Descartes (angle incident=angle réfléchi). Il s’agit bien du mouvement de la bille d’un « flipper », rebondissant sur les obstacles (modèle sans gravité, sans phénomène d'accélération ni de décélération). Supposons que les obstacles sont donnés par $(O_i+\ell,\ i=1,...,I,\ \ell\in\mathbb Z^2)$.

On se place dans le cadre des modèles à {{horizon fini}} en  supposant que la trajectoire de toute particule rencontre au moins un obstacle et on s’intéresse à la position d’une particule après un certain nombre de réflexions. On note donc $\mathcal C_\ell$ la cellule $\ell$ donnée par $\mathcal C_\ell=\bigcup_{i=1}^I(O_i+\ell)$, et, pour une configuration initiale $x$, c’est à dire un couple position vitesse $x=(q,\vec v)$, on note $S_n(x)$ l'indice de la cellule dans laquelle se trouve la particule à l'instant de la $n$-ème réflexion :

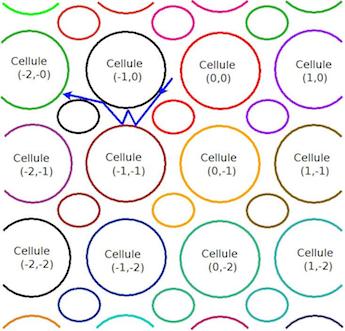
L’aléa mis sur la configuration initiale est modélisé par une mesure de probabilité $P$ absolument continue par rapport à la mesure de Lebesgue. De nombreux résultats montrent que, sous $\mathbb P$, $(S_n-S_0)_n$ se comporte asymptotiquement comme $(X_1+...+X_n)_n$ où $(X_i)_i$ est une suite de variables aléatoires indépendantes, de même loi, centrées et de carrés intégrables, à valeurs dans $\mathbb Z^2$. Par exemple, [2,1,11] ont montré que $(S_n)_n$ vérifie un théorème central limite:
$$\frac{S_n-S_0}{\sqrt {n}} \stackrel{\mbox{en loi}}{\longrightarrow} B,$$
où $B$ est une variable aléatoire de loi normale et [10] a montré les théorèmes limites locaux suivants:
$$\mathbb P(S_n=S_0)\sim \phi_B(0) n^{-1}\quad\mbox{et}\quad\mathbb P(S_n= S_{n+m}=S_0)\sim (\phi_B(0))^2 n^{-1}m^{-1}, $$
lorsque $n$ et $m$ tendent vers l'infini, en notant $\phi_B$ la densité de la loi de $B$.
Ces deux résultats portant sur des probabilités de retour à la cellule initiale leur ont permis de montrer que le gaz de Lorentz est récurrent, c'est-à-dire qu'il repasse infiniment souvent dans la cellule initiale (voir aussi [3]).

Mais un véritable modèle de "flipper" nécessite d’ajouter à ce processus des trajectoires du gaz de Lorentz une notion de gain lors des chocs sur les obstacles. On rajoute donc  dans les hypothèses que la particule gagne une valeur réelle $F(\ell)$ à chaque instant où elle touche un obstacle de la cellule $\mathcal C_\ell$ :

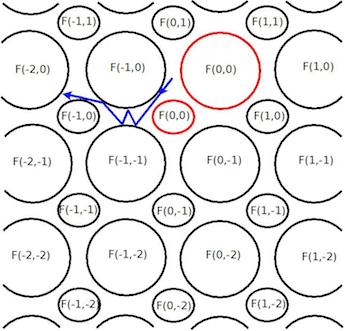
La somme totale $Z_n$ gagnée après la $n$-ème réflexion à ce jeu de {flipper infini} est $Z_n:=\sum_{k=1}^nF(S_k)$.
Si  les $F(\ell)$ sont sommables, alors il a été démontré dans [5] que
$$\frac {Z_n}{\ln n}\stackrel{\mbox{en loi}}{\longrightarrow} \phi_B(0)\, \sum_{\ell\in\mathbb Z^2}F(\ell).\, \mathcal E\, ,$$
où $\mathcal E$ est une variable aléatoire de loi exponentielle de paramètre 1.

Françoise Pène et Damien Thomine se sont intéressés dans [9] au cas où la somme est nulle:$$\sum_{\ell\in\mathbb Z^2}F(\ell)=0.$$
En supposant de plus la sommabilité des $|\ell|^\varepsilon |F(\ell)|$ pour un $\varepsilon>0$, ils obtiennent que
$$\frac {Z_n}{\sqrt{\ln n}}\stackrel{\mbox{en loi}}{\longrightarrow}\sqrt {\phi_B(0) }\, \sigma (F)\, \sqrt{\mathcal E}\, Z\, ,$$
où $\mathcal E$ et $Z$ sont deux variables aléatoires indépendantes avec $Z $ de loi normale centrée réduite et $\mathcal E $ comme précédemment. Le terme $ \sigma (F)$ est une constante explicite [[La formule donnant $\sigma(F)$ est une généralisation en mesure infinie d'une formule classique en mesure finie (formule de Green-Kubo): $\sigma^2(F)=\sum_{k\in\mathbb Z}\int F(S_0)F(S_k)\, d\tilde\mu $ pour une certaine mesure $\sigma $-finie $\tilde\mu $. La mesure $\tilde \mu$ est la mesure absolument continue par rapport à la mesure de Lebesgue et invariante par l'application $\tilde T$ qui, à un vecteur réfléchi (pour le gaz de Lorentz), associe le vecteur réfléchi à l'instant de la réflexion suivante.]].
Remarquons que la normalisation de $Z_n $ est alors  en $\sqrt {\sum_{k=1}^n\mathbb P (S_k=0)}$ alors qu'elle est en $\sum_{k=1}^n\mathbb P (S_k=0)$ si la somme n'est pas nulle.
Françoise Pène et Damien Thomine démontrent ce résultat à l'aide de versions spectrales du théorème limite local. Leur preuve originale et générale apporte une alternative aux preuves existantes dans les cas classiques où $(S_n )_n $ est une marche aléatoire ou une chaîne de Markov [4,7,6]. Leur résultat entre dans le cadre des théorèmes centraux limites pour des systèmes ergodiques en mesure infinie, dont l'étude est actuellement en plein développement.