Les mathématiques et le contrôle optimal à l’assaut du cancer

Traiter efficacement un cancer par chimiothérapie est une véritable gageure pour les oncologues. La première difficulté provient de la toxicité des traitements pour les cellules saines. La résistance au traitement en est le deuxième écueil : même s’il peut initialement faire décroître la tumeur, c’est au prix de la sélection des cellules les plus résistantes aux dépens des autres. La tumeur résiduelle est donc insensible à la poursuite de la chimiothérapie et peut croître à nouveau. Quelle doit donc être la stratégie pour faire décroître la tumeur le plus possible ? Il s’agit de choisir les doses de médicaments au cours du temps de manière à minimiser, au terme de cette période, la taille de la tumeur. Les stratégies très offensives, avec administration de fortes doses pendant de longues périodes, sont aujourd’hui remises en cause. Des alternatives, avec des périodes sans traitement ou de longues phases à faibles doses, émergent.

Ce problème a été modélisé par Camille Pouchol, Jean Clairambault, Alexander Lorz et Emmanuel Trélat sous forme d’un problème de contrôle optimal dans [1], dans lequel la résistance est représentée par une variable continue $x\in [0,1]$ appelée phénotype, variant continûment de la sensibilité maximale au traitement $(x=0)$ jusqu’à la résistance maximale $(x=1)$. En effet, celle-ci peut être corrélée à des grandeurs biologiques continues (la concentration de transporteurs éliminant le médicament, par exemple). L’objet mathématique considéré est la densité de cellules $n(t,x)$ de phénotype $x$ à l’instant $t$. Le modèle est constitué d’un système d’équations s’appuyant sur le modèle de base
$$\frac{\partial n }{\partial t} =
(r(x)-a \rho(t)(t))  n(t,x)$$
où
$\rho(t)= \int_0^1 n(t,x)dx$  est le nombre total de cellules à l’instant $t$. C’est un modèle exponentiel dans lequel les cellules prolifèrent et meurent à un taux $r(x)$  qui dépend de leur phénotype $x$, mais ont aussi un taux de mort additionnel $a \rho(t)$ dit logistique, proportionnel au nombre total de cellules. Ce terme modélise la compétition entre les cellules.
Ces modèles ont le comportement asymptotique suivant : le nombre total $\rho(t)$ de cellules converge et il y a concentration de $n(t,⋅)$  sur les phénotypes qui ont un avantage sélectif, i.e., qui réalisent le maximum de la fonction $r$. Si ce maximum est unique, $n(t,⋅)$  converge ainsi vers une masse de Dirac en ce phénotype.

Dans [1], les auteurs considèrent un système de deux équations couplées de ce type. Les variables sont les densités de cellules saines et cancéreuses $n_H (t,x)$ et $n_C (t,x)$. La chimiothérapie est prise en compte via deux contrôles $u_1 (t)$ et $u_2 (t)$  modélisant respectivement des agents cytotoxiques (qui tuent les cellules), et cytostatiques (qui ralentissent leur prolifération). Ceux-ci ne peuvent excéder certaines doses, appelées doses maximales tolérées.

La première tâche du travail consiste à s’assurer que ce modèle reproduit, à hautes doses constantes de chimiothérapie, ce qui est observé en clinique : un effet délétère sur le tissu sain et l’émergence d’une tumeur résistante. Cette question est étudiée en procédant à l’analyse asymptotique du modèle, et en démontrant qu’il vérifie aussi les propriétés de convergence pour $\rho_H (t)$ (resp. $\rho_C (t))$, le nombre total de cellules saines (resp., cancéreuses), et de concentration sur certains phénotypes pour $n_H (t,x)$ et $n_C (t,x)$. Numériquement, on observe effectivement qu’avec de hautes doses $\rho _H$ décroît exponentiellement vite et $\rho_C$ décroît puis croît rapidement. Ce phénomène est dû à la convergence de $n_C (t) $ vers une masse de Dirac localisée sur un phénotype résistant. La Figure 1 ci-dessous présente une mauvaise stratégie $\rho_{CS} (t)= \int_0^1(1-x) n_C (t,x)dx$, avec $T=10$. Pour $n_H$ et $ n_C,$ la condition initiale est en noir, la finale en rouge, avec en bleu la dynamique.

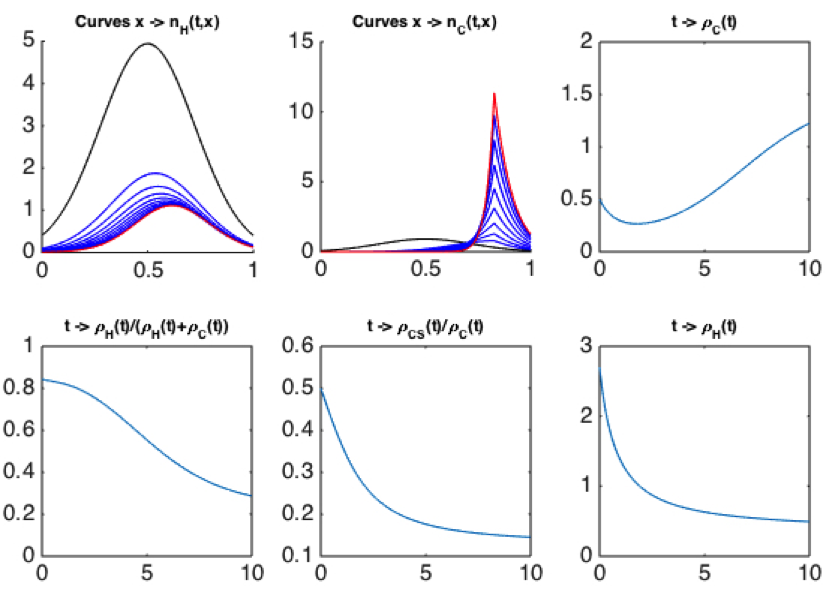
Cela justifie, au niveau du modèle, l’étude du problème de contrôle optimal consistant à minimiser le nombre total de cellules cancéreuses $\rho_C (T)$ à un instant $T$ fixé, avec des contrôles ne dépassant pas les doses maximales tolérées. Par ailleurs, nous imposons deux contraintes : le nombre de cellules saines et leur proportion $\rho_H/(\rho_H+\rho_C )$ doivent toujours excéder certains seuils.

Dans [1], les auteurs établissent que la stratégie optimale dans un horizon de temps $T$ est formée de deux phases principales. Celle-ci est illustrée par la Figure 2 et peut se résumer ainsi :
- la première phase, qui est longue, consiste à ajuster des doses médicamenteuses assez faibles et à attendre que la concentration (convergence vers une masse de Dirac) se fasse sur un phénotype sensible;
-  la seconde phase, qui est courte, consiste alors à utiliser les doses maximales pour tuer les cellules cancéreuses. Elles sont en effet optimales lorsque le phénotype est concentré.

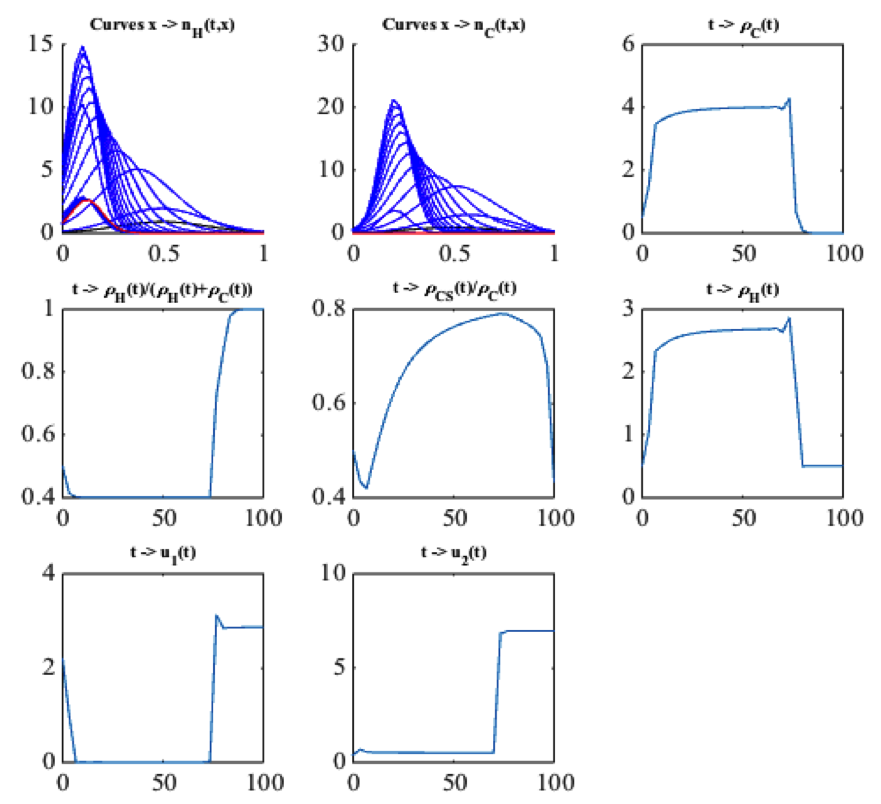
Des discussions sont en cours avec des cancérologues de l’Hôpital Tenon à Paris pour identifier les types de tumeurs qui se prêtent à l’application du modèle. L’objectif est de proposer une stratégie pseudo-périodique faite d’alternance de phases longues (à faibles doses) et courtes (à fortes doses) comme ci-dessus, le passage d’une phase à une autre se faisant en fonction d’indicateurs cliniques à définir.