La genèse des anneaux tourbillonnaires visqueux

Dans les études expérimentales et les simulations numériques des écoulements incompressibles, on observe la formation de structures tourbillonnaires cohérentes qui occupent une fraction relativement faible du volume disponible, mais sont responsables d'une part importante de la dissipation d'énergie. Ces structures correspondent à des zones de forte concentration du tourbillon du fluide, lequel est défini mathématiquement comme le rotationnel du champ de vitesse.

Les exemples les plus communs sont les tourbillons circulaires que l'on remarque à la surface des cours d'eau, notamment près des rives. En dimension trois, les structures les plus spectaculaires sont les anneaux tourbillonnaires, ou anneaux de fumée, que l'on peut observer au-dessus du cratère de certains volcans en activité, ou produire soi-même à plus petite échelle avec des dispositifs assez simples. Ces anneaux ont une forme toroïdale et se déplacent le long de leur axe de symétrie à une vitesse approximativement constante, sur des intervalles de temps remarquablement longs.

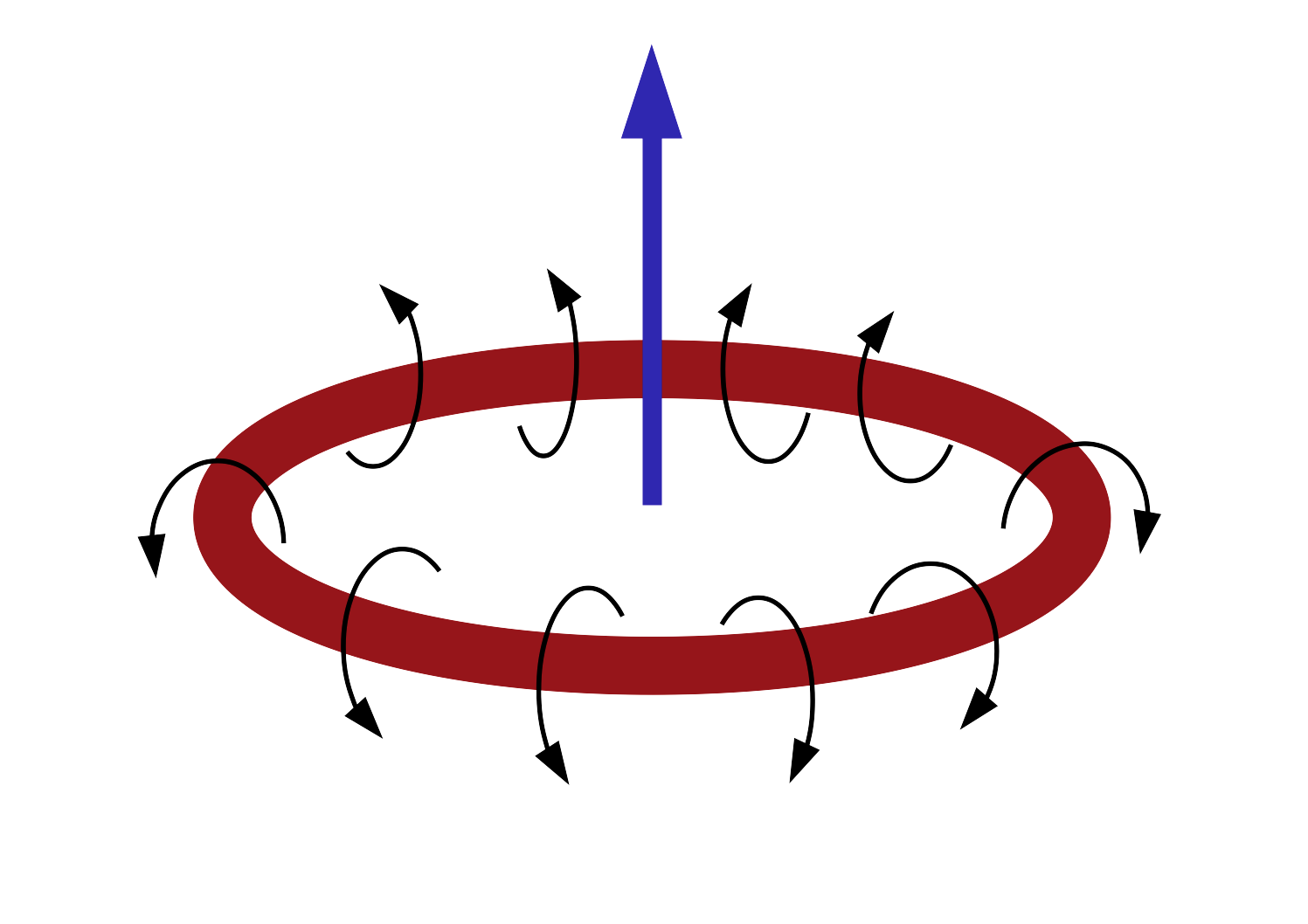
Pour étudier mathématiquement les anneaux tourbillonnaires, on se place dans le cadre des écoulements "axisymétriques sans swirl". Ceci signifie que le champ de vitesse du fluide est invariant par rotation autour d'un axe, que l'on supposera vertical, et de surcroît invariant par réflexion par rapport à n'importe quel plan contenant l'axe de symétrie, voir la figure 1 ci-dessous. Ce cadre géométrique offre de nombreuses analogies avec celui des écoulements plans. En particulier, on sait depuis les travaux de O. Ladyzhenskaya et de M. Ukhovskii & V. Yudovich (1968) que le problème de Cauchy est globalement bien posé dans le cadre axisymétrique sans swirl, aussi bien pour les équations de Navier-Stokes que pour les équations d'Euler.

En l'absence de viscosité, il est possible de construire des solutions de l'équation d'Euler qui sont stationnaires dans un référentiel en translation verticale et dont le tourbillon est effectivement concentré dans un tore plein. Les premiers résultats rigoureux dans cette direction ont été obtenus par L. E. Fraenkel en 1970 [3], et de nombreux progrès ont été réalisés depuis en utilisant notamment des techniques variationnelles. Dans une perspective un peu différente, D. Benedetto, E. Caglioti, and C. Marchioro [2] ont montré que, pour toute donnée initiale dont le tourbillon est concentré dans un tore plein de section suffisamment petite, la solution des équations d'Euler conserve une telle propriété de localisation sur un certain intervalle de temps, et décrit donc le mouvement d'un anneau tourbillonnaire.

Dans le cas visqueux, la dissipation de l'énergie exclut évidemment l'existence de solutions stationnaires dans un référentiel en mouvement. En revanche, il est possible de résoudre le problème de Cauchy avec un filament circulaire pour donnée initiale, ce qui signifie que le tourbillon initial est une mesure concentrée sur un cercle [4]. L'unique solution des équations de Navier-Stokes décrit alors un anneau tourbillonnaire visqueux, de profil gaussien, qui se déplace le long de son axe à une vitesse prédite par L. Kelvin (1867) et P. G. Saffman (1970). Il existe en fait une famille à un paramètre de telles solutions, indexée par un nombre de Reynolds défini dans ce contexte comme le rapport Γ/ν, où Γ est la circulation du filament initial et ν la viscosité cinématique du fluide. De façon surprenante, l'article [5] fournit une description asymptotique de la solution valable sur un intervalle de temps qui augmente sans limite lorsque le nombre de Reynolds tend vers l'infini.

Plus généralement, il est possible d'étudier la solution des équations de Navier-Stokes lorsque le tourbillon initial est un filament de forme quelconque, non nécessairement circulaire [1]. Une conjecture importante affirme que la solution à grand nombre de Reynolds reste concentrée au voisinage d'une courbe qui évolue selon le flot binormal (un analogue hamiltonien du flot de courbure moyenne). L'article [5] résout donc cette conjecture dans le cadre très particulier des solutions axisymétriques sans swirl.