The genesis of viscous vortex rings

In experimental studies and numerical simulations of incompressible flows, we observe the formation of coherent vortex structures that occupy a relatively small fraction of the available volume, but are responsible for a significant proportion of energy dissipation. These structures correspond to zones of high fluid vortex concentration, defined mathematically as the rotational velocity field.

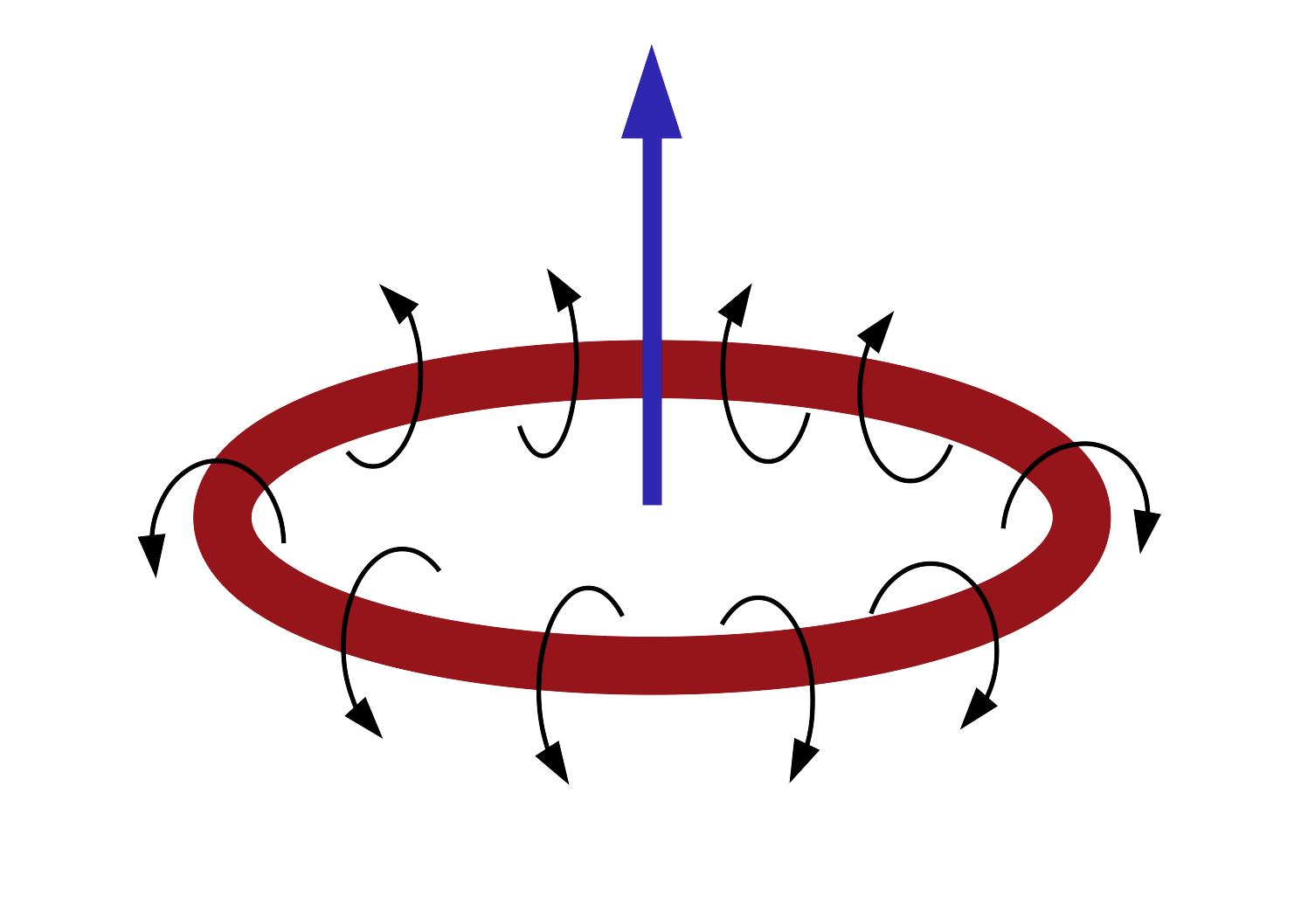
The most common examples are the circular vortices seen on the surface of rivers, especially near their banks. In dimension three, the most spectacular structures are the vortex rings, or smoke rings, which can be observed above the craters of certain active volcanoes, or produced by ourselves on a smaller scale with fairly simple devices. These rings have a toroidal shape and move along their axis of symmetry at an approximately constant speed, over remarkably long time intervals.

To study vortex rings mathematically, we place ourselves in the framework of “axisymmetric swirl-free” flows.

This means that the fluid velocity field is invariant by rotation around an axis, which we'll assume to be vertical, and moreover invariant by reflection with respect to any plane containing the axis of symmetry, see Figure 1 below. This geometrical framework offers many analogies with that of plane flows. In particular, since the work of O. Ladyzhenskaya and M. Ukhovskii & V. Yudovich (1968) that the Cauchy problem is globally well posed in the axisymmetric framework without swirl, for both the Navier-Stokes and Euler equations.

In the absence of viscosity, it is possible to construct solutions of the Euler equation that are stationary in a vertically translating reference frame and whose vortex is effectively concentrated in a full torus. The first rigorous results in this direction were obtained by L. E. Fraenkel in 1970 [3], and much progress has since been made using variational techniques in particular. From a slightly different perspective, D. Benedetto, E. Caglioti, and C. Marchioro [2] have shown that, for any initial data whose vortex is concentrated in a full torus of sufficiently small cross-section, the solution of Euler's equations retains such a localization property over a certain time interval, and thus describes the motion of a vortex ring.

In the viscous case, energy dissipation obviously rules out the existence of stationary solutions in a moving frame of reference. On the other hand, it is possible to solve the Cauchy problem with a circular filament as initial data, which means that the initial vortex is a measure concentrated on a circle [4]. The unique solution of the Navier-Stokes equations then describes a viscous vortex ring with a Gaussian profile, moving along its axis at a speed predicted by L. Kelvin (1867) and P. G. Saffman (1970). There is in fact a one-parameter family of such solutions, indexed by a Reynolds number defined in this context as the ratio Γ/ν, where Γ is the initial filament circulation and ν the kinematic viscosity of the fluid. Surprisingly, the paper [5] provides an asymptotic description of the solution valid over a time interval that increases without limit as the Reynolds number tends towards infinity.

More generally, it is possible to study the solution of the Navier-Stokes equations when the initial vortex is a filament of any shape, not necessarily circular [1].

An important conjecture asserts that the solution at high Reynolds numbers remains concentrated in the vicinity of a curve that evolves according to the binormal flow (a Hamiltonian analogue of the mean-curvature flow). The paper [5] solves this conjecture in the very special context of axisymmetric solutions without swirls.