Maths & Musique #1 : Les maths dans la musique, la musique des maths : réflexions autour de la « dynamique mathémusicale », par Moreno Andreatta

Voilà une question qui aurait sans doute fait sourire les scientifiques et musiciennes ou musiciens professionnels il y a juste une trentaine d’année, la musique étant souvent considérée comme un divertissement et les maths comme une discipline trop rigide pour pouvoir jouer un rôle dans la créativité musicale. Les temps ont bien changé depuis le lancement, en 2007, de la première revue à comité de lecture sur les rapports mathématiques/musique (le Journal of Mathematics and Music), organe officiel de la Society for Mathematics and Computation in Music. A cela s’est ajoutée l’inscription, quelques années plus tard, de ce domaine de recherche au sein de la Mathematical Subject Classification (avec le code 00A65).

Mais ce qui a changé a été surtout la prise de conscience, de la part des mathématiciennes ou mathématiciens et des musiciennes ou musiciens, de l’existence de problèmes difficiles posés par la musique et susceptibles de faire avancer la recherche en mathématiques. En même temps la souplesse et généralité des concepts et constructions mathématiques ont suggéré aux artistes l’intérêt d’un travail de formalisation et modélisation des problèmes théoriques posés par la musique. La mise en évidence de tels problèmes musicaux constitue le point de départ d’une véritable « dynamique mathémusicale ».

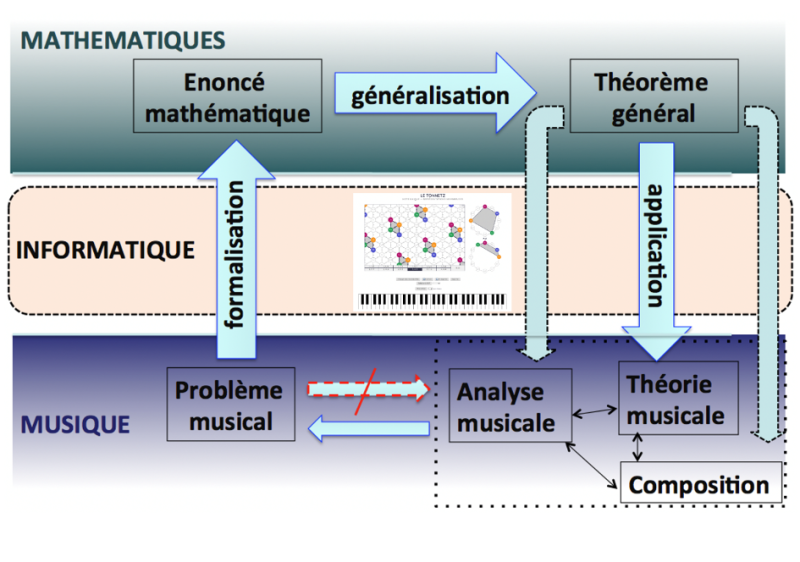
Ce processus commence par la formalisation du problème théorique à travers une panoplie d’outils issus de plusieurs branches des mathématiques. Elle permet d’obtenir un énoncé mathématique, première étape vers une généralisation qui peut aboutir à des théorèmes. Ces résultats généraux pourront à leur tour être appliqués à la théorie, analyse et composition musicales. Dans ce processus on traverse une région qui constitue une interface entre la musique et les mathématiques. C’est l’espace de la modélisation informatique, qui consiste parfois dans l’implémentation des résultats théoriques obtenus en vue de leurs applications musicales.

On pourrait citer plusieurs exemples de problèmes théoriques à la base de cette dynamique, de la construction des canons musicaux dits « mosaïques » aux représentations géométriques et topologiques des espaces harmoniques ou rythmiques. Sans entrer dans les aspects techniques des outils mathématiques employés, dans les deux cas on assiste à une articulation féconde entre la formalisation algébrique du problème musical et la modélisation informatique. Cette articulation est au cœur du projet SMIR (Structural Music Information Research) mené à présent à l’université de Strasbourg, en collaboration étroite avec l’équipe Représentations musicales de l’Ircam (UMR STMS). Dans le cadre de ce projet, nous avons concentré nos efforts dans le développement d’environnements interactifs open source et accessibles en ligne car ils facilitent à la fois l’apprentissage des savoirs mathémusicaux mais aussi l’application des nouvelles constructions théoriques dans le domaine de la créativité musicale. C’est le cas, par exemple, de l’environnement TONNETZ qui permet de visualiser les notes de musique et les accords à la fois à travers des représentations bien connues par les musiciens (cercle chromatique et cycle des quintes) mais aussi à travers des espaces à deux dimensions. Ces réseaux de notes sont issus des possibles décompositions du plan par des triangles selon des axes qui correspondent aux divers intervalles musicaux. Cette idée remonte à Léonard Euler, théoricien de la musique et mathématicien du XVIII^e siècle, qui avait associé aux axes générateurs du plan la tierce majeure et la quinte juste, deux parmi les intervalles les plus consonants et qui sont à la base de l’accord majeur.

Aujourd’hui, on généralise cette approche afin de représenter un accord musical en fonction de l’espace géométrique permettant de mettre en évidence les diverses symétries qui le composent. Certaines progressions d’accords peuvent ainsi être formalisées comme des trajectoires spatiales dans le graphe associé à ce réseau de notes ou Tonnetz. Dans ce graphe on peut aisément passer du pavage triangulaire au pavage hexagonal correspondant ou maillage à nid d’abeilles dans lequel les arcs reliant les sommets correspondent aux symétries entre accords qui préservent deux notes sur trois des accords respectifs.

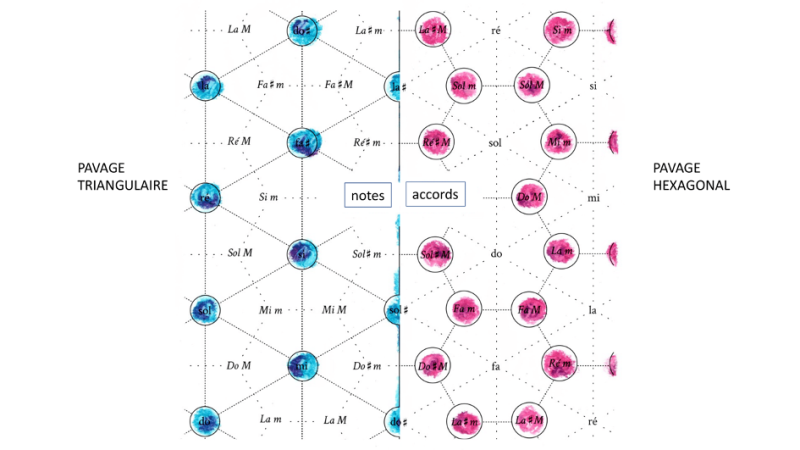
On peut ainsi se poser la question de la recherche des boucles harmoniques correspondant à des trajectoires spatiales dans le Tonnetz qui permettent de passer une et une seule fois par chaque accord, avant de revenir au point initial. C’est l’équivalent, en musique, du problème du cavalier dans le jeu d’échecs, consistant à trouver un parcours permettant à cette pièce de passer une et une seule fois par toutes les cases de l’échiquier avant de revenir au point de départ. En musique, un tel procédé est à la base des chansons dites « hamiltoniennes », des chansons dans lesquelles on peut moduler dans les vingt-quatre tonalités majeures et mineures sans répéter deux fois le même type d’accord On est bien au-delà des trois ou quatre accords qui constituent la plupart des tubes que nous avons l’habitude d’entendre. Le résultat final n’a rien d’artificiel, comme le lecteur pourra constater en écoutant, par exemple, la chanson hamiltonienne « Le blé en herbe » de Polo Lamy, disponible sur ma chaîne Youtube.

Mais, au-delà des spécialistes en mathématiques ou en musique, peut-on arriver à transmettre les savoirs mathémusicaux a un public n’ayant aucune connaissance approfondie ni des maths ni de la musique ? C’est le défi que nous essayons de relever à présent à travers le projet LaMaMu, soutenu par l'IDEX "Sciences et société et en territoire" de l'université de Strasbourg et le CREAA, qui déploie une série d’actions à destination des élèves de collège et lycée ainsi que du grand public. Des ateliers pédagogiques réalisés en partenariat avec des enseignants relevant du dispositif LaboMath du ministère de l’éducation nationale permettent aux élèves de se familiariser avec plusieurs concepts de mathématiques à partir de la musique. Les mêmes constructions théoriques à la base des ateliers scolaires sont également reprises dans le spectacle Math’n Pop, initialement labellisé par le CNRS dans le cadre des célébrations pour ses 80 ans.

Cette conférence-concert théâtralisée propose une mise en scène d’idées et concepts mathématiques à partir de la musique, porte d’entrée privilégiée pour faire aimer les maths au grand public. D’autres initiatives en direction du grand public sont en cours comme, par exemple, la rédaction du célèbre calendrier mathématique, dont l’édition 2025 sera consacrée à la mathémusique. Une occasion précieuse pour découvrir, tous les mois, un sujet qui touche aux différents aspects des rapports mathématiques/musique, avec une série de défis mathématiques qui permettront au lecteur de s’approprier progressivement quelques idées à la base de cette inépuisable dynamique mathémusicale.