Maths & Musique #6 : Mathématiques des canons rythmiques

Il s’avère que ces canons sont liés à des problèmes ardus de mathématique, et même à des conjectures ouvertes sur lesquelles les problématiques des musiciennes et musiciens ont permis de faire des progrès substantiels. 

Un canon rythmique est analogue à un canon classique mais on ne tient compte que de la durée des notes et non de leur hauteur : seul le rythme est répété. Un canon rythmique est mosaïque lorsqu’à chaque moment du déroulement du canon on entend une et une seule note du rythme de base (il n’y a ni recouvrement ni silence). Cela correspond à un pavage de l’axe du temps (les entiers) par les voix du canon.

Exemple : Le motif (0 1 4 5) correspond à des notes aux temps 0 et 1, suivies par deux silences aux temps 2 et 3, puis deux notes aux temps 4 et 5. On peut créer un canon mosaïque avec deux copies de ce motif : le motif initial (0 1 4 5) et le même motif décalé de deux temps (2 3 6 7). Leur réunion (0 1 2 3 4 5 6 7) forme une séquence à la fois pleine et sans redondance des temps 0 à 7, on peut donc bien obtenir un pavage des entiers en les répétant indéfiniment.

On parle de pavage par translation et on note (0 1 4 5) + (0 2) = (0 1 2 3 4 5 6 7).

Essayez avec (0 4 8) ! Est-ce que vous y arrivez avec (0 1 6) ?

Plus intéressants, les pavages circulaires, ou périodiques. La définition mathématique nécessite de calculer avec un modulo. Vous connaissez le modulo 12 qui est utilisé sur toutes les montres avec des aiguilles : 13 h s’identifie à 1 h, 16 h à 4 h, etc. Un exemple de motif qui pave modulo 12 est (0 1 3 6); En effet, la réunion du motif initial et de ses 2 copies décalées de 4 et de 8, donne

(0 1 3 6) + (0 4 8) = (0 1 3 4 5 6 7 8 9 10 11 14)

mais comme 14 est identifié à 2, on obtient bien (0 1 2 3 4 5 6 7 8 9 10 11), un pavage des temps 0 à 11.

En représentant ce pavage sur une horloge tout devient plus clair : sur la figure, le quadrilatère bleu correspond au motif initial, avec Jacques qui sonne sa cloche à 0, 1, 3 et 6 heures ; le quadrilatère rouge correspond au motif initial décalé de 4, avec Paule qui sonne sa cloche à 4, 5, 7 et 10 heures ; enfin, le quadrilatère gris correspond au motif initial décalé de 8, avec Pierre qui sonne sa cloche aux heures restantes. Quand la troisième voix est rentrée, le canon procède sans plus laisser de silences.

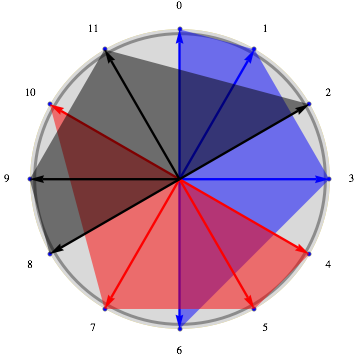
Mathématiquement, un motif A pave modulo n s’il existe un ensemble d’entrées B tel que A + B soit égal à l’ensemble de toutes les valeurs modulo n, chacune étant atteinte une fois et une seule. 

Comme c’est si souvent le cas, exprimer le problème mathématiquement permet d’en déduire une foule de résultats que l’intuition ne nous avait pas donnés. Ainsi de la dualité : si on a A + B = (0, 1… n-1) alors sans effort supplémentaire il vient B + A = (0, 1… n-1), ce qui signifie qu’on a aussi un canon rythmique dont le motif est B avec A  comme entrées. En reprenant l’exemple précédent, cela donne un canon à quatre voix au lieu de trois, dit canon dual :

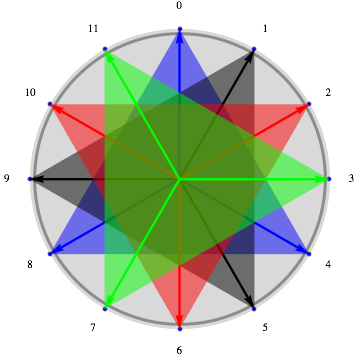
Les pavages d’horloges sont riches en problèmes ouverts : par exemple, il n’existe pas de formule pour les donner tous, ou pour les dénombrer, ou d’algorithme efficace pour déterminer si un motif quelconque réalise un pavage (tout au plus on peut deviner la taille de l’horloge, mais celle-ci peut être considérablement plus grande que le motif).

Dan Tudor Vuza, mathématicien roumain intéressé par la musique via notamment son ami le compositeur et théoricien Anatol Vieru, a réussi le tour de force de construire seul, à l’est du rideau de fer, la théorie des canons rythmiques sans savoir que des mathématiciens occidentaux avaient élaboré la théorie isomorphe des pavages par translation. 

L’angle musical lui a permis de souligner une capacité auditive passée inaperçue des mathématiciens « purs », celle de réduire le motif ou le motif des entrées à sa plus simple expression : dans la plupart des canons/pavages, l’un ou l’autre facteur s’avère périodique, c’est à dire qu’on peut réduire le canon à la répétition régulière d’un motif irrégulier minimal, celui que l’oreille perçoit comme « le » motif.

On a même conjecturé, à tort (Hajós, 1950) que c’était toujours le cas. Vuza a (re)découvert des contre-exemples — très rares ! — et une construction possible pour des pavages des cercles divisés en 72, 108, 120, 1441 … Tout pavage périodique par translation peut se réduire à l’un de ces « canons de Vuza », un peu comme tout nombre entier se décompose en produits de facteurs premiers. Ils jouent donc un rôle central dans l’étude des pavages, et ont permis d’avancer substantiellement sur un certain nombre de problèmes ouverts, comme la conjecture de Fuglede ou la « conjecture T2 ».

Enfin, il existe des motifs qui ne peuvent pas réaliser de canons rythmiques par translation, comme (0 3 4 6), mais le permettent si on ajoute la forme rétrogradée du motif, obtenue en inversant le motif, ici (0 2 3 6).

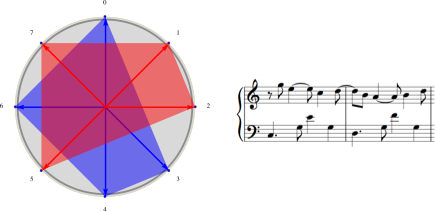
Rythmiquement il s’agit du rythme nonchalant de la habanera commun en Tango et ailleurs. Astor Piazzola a joué avec des pavages rythmiques (avec redondances) autour de ce rythme fondamental et quelques autres classiques, comme le tresillo (cf. Libertango, par exemple).

• 1https://oeis.org/A102562

Un résultat remarquable prouve qu’on peut toujours réaliser un pavage avec rétrogradation pour n’importe quel motif de trois notes. En revanche c’est impossible avec, par exemple, (0 1 3 4) pour lequel la rétrogradation n’apporte rien (voyez-vous pourquoi ?). Dans ce cas, il est possible d’utiliser un autre procédé déjà utilisé par certains compositeurs de la Renaissance, et aussi par J.S. Bach dans ses canons et fugues : l’augmentation, qui consiste à multiplier le motif par un facteur. Cela marche avec (0 1 3 4) (les trois solutions minimales m’ont permis de composer un chœur remixant une vieille balade irlandaise), bien que l’on ignore si pour tout motif il existe un pavage n’utilisant qu’un nombre fini d’augmentations. Un exemple plus simple est dû au compositeur Tom Johnson. On peut paver avec (0 1 4) et son augmentation par 2, (0 2 8) comme par exemple :

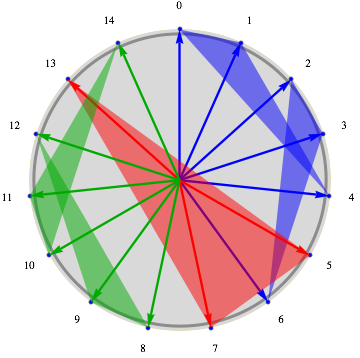
À l’aide d’un programme écrit par A. Tangian, Johnson a pu observer que toutes les solutions avec des augmentations par 2, 4, 8, 16… avaient un nombre de notes multiple de 15. C’est en mettant plus d’un an à démontrer ce résultat d’apparence très simple que je me suis passionné pour l’étude des canons rythmiques !