Maths & Music #6: Mathematics of rhythmic canons

It turns out that these canons are linked to arduous mathematical problems, and even to open conjectures on which the problems of musicians have enabled substantial progress to be made.

A rhythmic canon is analogous to a classical canon, but only the duration of the notes is taken into account, not their pitch: only the rhythm is repeated. A rhythmic canon is mosaic when one and only one note of the basic rhythm is heard at each moment in the course of the canon (there are no overlaps or silences). This corresponds to a tiling of the time axis (the integers) by the voices of the canon.

Example: The pattern (0 1 4 5) corresponds to notes at beats 0 and 1, followed by two silences at beats 2 and 3, then two notes at beats 4 and 5. A mosaic canon can be created with two copies of this pattern: the initial pattern (0 1 4 5) and the same pattern shifted by two beats (2 3 6 7). Their union (0 1 2 3 4 5 6 7) forms a full, redundancy-free sequence of beats 0 to 7, so we can obtain a tessellation of integers by repeating them indefinitely.

We speak of translational paving and note (0 1 4 5) + (0 2) = (0 1 2 3 4 5 6 7).

Try it with (0 4 8)! Can you do it with (0 1 6)?

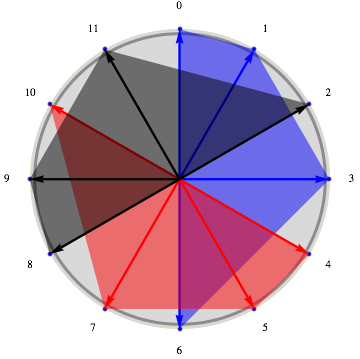
More interesting are circular or periodic tessellations. The mathematical definition requires you to calculate with a modulo. You're familiar with the modulo 12 used on all watches with hands: 13 o'clock identifies 1 o'clock, 16 o'clock 4 o'clock, and so on. An example of a pattern that paves modulo 12 is (0 1 3 6); in fact, reuniting the initial pattern with its 2 copies, shifted by 4 and 8, gives

(0 1 3 6) + (0 4 8) = (0 1 3 4 5 6 7 8 9 10 11 14)

but since 14 is identified with 2, we get (0 1 2 3 4 5 6 7 8 9 10 11), a tessellation of beats 0 to 11.

By representing this paving on a clock, everything becomes clearer: on the figure, the blue quadrilateral corresponds to the initial pattern, with Jacques ringing his bell at 0, 1, 3 and 6 o'clock; the red quadrilateral corresponds to the initial pattern shifted by 4, with Paule ringing her bell at 4, 5, 7 and 10 o'clock; finally, the gray quadrilateral corresponds to the initial pattern shifted by 8, with Pierre ringing his bell at the remaining hours. Once the third voice has entered, the canon proceeds without further silences.

Mathematically, a pattern A paves modulo n if there is a set of inputs B such that A + B is equal to the set of all values modulo n, each reached once and only once.

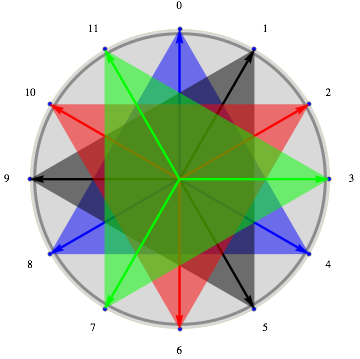
As is so often the case, expressing the problem mathematically allows us to deduce a host of results that intuition hadn't given us. For example, if we have A + B = (0, 1... n-1), then without further effort we have B + A = (0, 1... n-1), which means that we also have a rhythmic canon whose motif is B, with A as input. Taking the previous example, this gives a canon with four voices instead of three, known as a dual canon :

Clock tessellations are rich in open problems: for example, there is no formula to give them all, or to count them, or an efficient algorithm to determine whether any pattern achieves a tessellation (at most, we can guess the size of the clock, but this can be considerably larger than the pattern).

Dan Tudor Vuza, a Romanian mathematician interested in music via his friend the composer and theorist Anatol Vieru, succeeded in building the theory of rhythmic canons alone, east of the Iron Curtain, without knowing that Western mathematicians had elaborated the isomorphic theory of translational tilings.

The musical angle enabled him to highlight an aural capacity that had gone unnoticed by “pure” mathematicians, that of reducing the motif or pattern of entries to its simplest expression: in most canons/pavings, one or other factor turns out to be periodic, i.e. the canon can be reduced to the regular repetition of a minimal irregular motif, the one that the ear perceives as “the” motif.

It was even wrongly conjectured (Hajós, 1950) that this was always the case. Vuza (re)discovered counter-examples - very rare! - and a possible construction for tessellations of circles divided into 72, 108, 120, 1441 ... Any periodic tessellation by translation can be reduced to one of these “Vuza canons”, in much the same way as any integer can be decomposed into products of prime factors. They therefore play a central role in the study of tessellations, and have enabled substantial progress to be made on a number of open problems, such as the Fuglede conjecture or the “T2 conjecture”.

Finally, there are patterns that cannot realize rhythmic canons by translation, such as (0 3 4 6), but do if we add the retrograde form of the pattern, obtained by inverting the pattern, in this case (0 2 3 6).

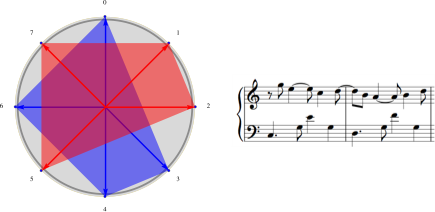
Rhythmically, it's the nonchalant habanera rhythm common to Tango and elsewhere. Astor Piazzola played with rhythmic paving (with redundancies) around this fundamental rhythm and a few other classics, such as the tresillo (cf. Libertango, for example).

• 1https://oeis.org/A102562

A remarkable result shows that tessellation with retrogradation is always possible for any three-note pattern. On the other hand, it's impossible with, say, (0 1 3 4), for which retrogradation brings nothing (can you see why?). In this case, it's possible to use another procedure already used by certain Renaissance composers, and also by J.S. Bach in his canons and fugues: augmentation, which consists in multiplying the motif by a factor. This works with (0 1 3 4) (the three minimal solutions enabled me to compose a chorus remixing an old Irish ballad), although we don't know whether for any pattern there exists a paving using only a finite number of augmentations. A simpler example comes from composer Tom Johnson. We can pave with (0 1 4) and its augmentation by 2, (0 2 8), for example :

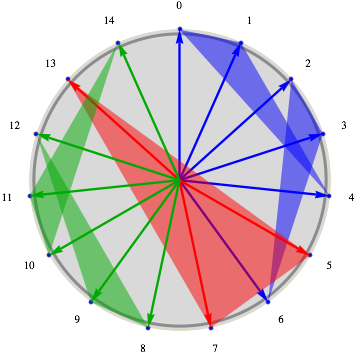
Using a program written by A. Tangian, Johnson was able to observe that all solutions with increments by 2, 4, 8, 16... had a number of notes that was a multiple of 15. It took me over a year to demonstrate this seemingly simple result, and I became fascinated by the study of rhythmic canons!