Maths & Musique #7 : Tempérament adaptatif en musique juste

« Pourquoi certaines notes jouées ensemble sonnent-elles harmonieusement et les accords formés ont des couleurs si variées ? » Écrit à deux voix, nous présentons dans cet article quelques aspects de ce sujet très riche ainsi que le « tempérament adaptatif», fruit d’une collaboration entre un musicien et un mathématicien. 

Dans le système musical occidental actuel, une octave est un rapport de fréquence 2/1 et chaque octave est divisée en 12 parties égales sur une échelle logarithmique appelé demi-ton, donnant l’échelle chromatique aussi appelé le tempérament égal. Ces douze notes sont appelées do,do#,ré,ré#,mi,fa,fa#,sol,sol#,la,la#,si ou C,C#,D,D#,E,F,F#,G,G#,A,A#,B. Ainsi partant de la fréquence du la (A) qui est f_A= 440 Hz, appelé diapason, on obtient f_A# = f_A2^1/12= 466 Hz, f_B=f_A2^2/12= 494 Hz etc.

Tempéraments fixes justes

Dans un autre système musical appelé musique juste, les notes ont des rapports de fréquences mutuels qui sont des fractions a/b avec des petits entiers a, b. Ces rapports de fréquences sont aussi appelés intervalles justes (ou purs). Les plus utilisés sont l’octave 2/1, la quinte 3/2, la quarte 4/3, la tierce majeure 5/4, etc. N’oublions pas l’unisson 1/1. Ce système est assez universel car ces intervalles justes sont perçus comme « résonnant » pour des raisons psycho-acoustiques [5] [2]. Ce sont les intervalles entre les harmoniques de la voix.

Une question a dû se poser depuis des millénaires: parmi l’infinité des fractions existantes, quelles notes faut-il choisir pour fabriquer (ou accorder) un instrument de musique disposant de quelques cordes seulement? Un tel choix de notes s’appelle un tempérament fixe. On peut objecter que de façon pratique l’infini n’existe pas, la perception auditive des fréquences a une limitation. Cette limitation est cependant très fine, de l’ordre d’une centaine de notes différentes par octave ce qui est énorme et largement supérieur à l’échelle chromatique à 12 notes par octave. Le choix d’un tempérament fixe est un vaste sujet et dépend des cultures  [1, chap.5]. Au Sénégal, en musique mandingue, une kora est accordée selon différents choix possibles. La musique indienne possède des dizaines de raga différents. La musique arabe possède différents maqâms. En Europe une grande variété de tempéraments permettaient une grande richesse expressive [3].

Pour illustrer un problème essentiel rencontré avec les tempéraments fixes, la figure ci-dessous présente les tempéraments de Zarlino (1517-1590) et de Kepler (1571-1630) et montre que la recherche d’un tempérament juste et fixe universel est sans issue, comme un no go theorem [1, chap.5.10].

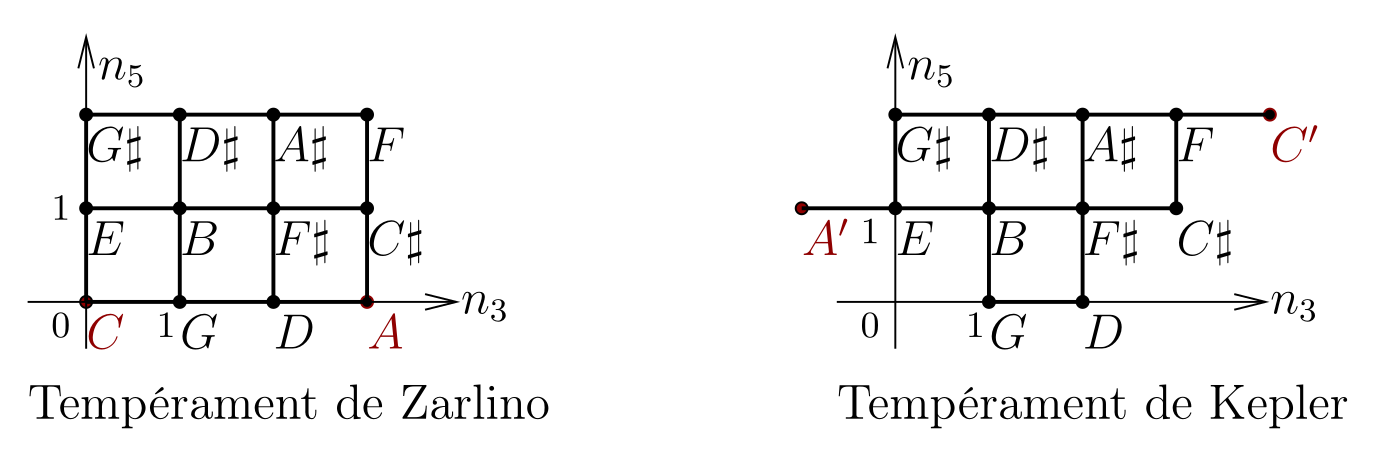
Le tempérament de Zarlino ou de Kepler est le choix de 12 notes par octaves (C, C#, D, …, B) dont les fréquences relatives sont déterminées par leur position précise sur un réseau ayant deux axes : l’axe des quintes n₃ et l’axe des tierces n₅. Plus précisément la fréquence f d’une note de coordonnées entières (n₃,n₅) est f=f_C2ⁿ²3ⁿ³5ⁿ⁵ où l’entier   dépend du choix de l’octave et f_C= 262 Hz est la fréquence de C (do). Le tempérament de Zarlino contient des quintes justes comme C --> G et des tierces comme C --> E mais ne possède pas la quinte F --> C ni A --> E. Pour avoir ces quintes, Kepler a modifié ce tempérament en déplaçant les choix C, A vers C', A'. Ce faisant on perd les quintes C --> G et D --> A et les tierces C --> E et A --> C#. Les petits écarts appelés comma sont (C-->C') = - 0.20 demi-ton (dt) et (AA') = - 0.22 dt  qui sont très perceptible. (explication: quinte = ln(3/2) / ln2^1/12 dt = 7 + 0.02 dt, tierce = 4 - 0.14 dt donc (CC')=(4 x 0.02-2 x 0.14) dt = - 0.20 dt.)

Tempérament égal non juste

L’impossible existence d’un tempérament à la fois juste et fixe a été vécu comme une impasse et a amené les musiciens et luthiers au XIXème siècle en occident à adopter collectivement le tempérament égal [1, chap.5.14, p.197] : le choix de douze notes par octaves équi-réparties sur l’échelle logarithmique des rapports de fréquences. Le rapport de fréquence entre deux notes distantes de n demi-tons est 2^n/12, ainsi avec un écart de n = 12 demi-tons on a le rapport (2^1/12)¹² = 2/1 qui est l’octave juste. Mais les autres écarts ne sont pas des fractions, ce sont des nombres irrationnels. Par exemple le triton (3 tons = 6 demi-tons) C --> F# est 2^6/12 = le fameux nombre irrationnel qui mit le trouble dans l’école de Pythagore. Ce qui fait la force de ce tempérament égal est que l’intervalle avec n = 5 demi-tons est très proche de la quarte juste : 2^5/12 = 1,3348... ~ 1,333... = 4/3 et l’intervalle avec n = 7 demi-tons est très proche de la quinte juste : 2^7/12 = 1,498... ~ 1,5 = 3/2 (ces écarts sont imperceptibles à notre audition). Ainsi le tempérament égal a probablement été adopté car il propose une construction avec des intervalles de quartes et quintes qui sont quasiment justes, et car il est invariant par translation ce qui correspond aux transpositions en musique. Cependant les tierces et autres intervalles justes utilisant les nombres premiers 5, 7, 11... seront mal exprimés. De nombreux courants musicaux en occident ont cherché à « rejouer » avec des intervalles plus fins comme les intervalles justes ou la musique micro-tonale.

Tempérament adaptatif juste et instruments adaptés

Le tempérament adaptatif proposé dans l’article [4] permet de jouer de la musique avec des intervalles justes et avec seulement 12 touches par octave: le choix des hauteurs des notes n’est pas fixe, mais peut varier avec le temps et est optimisé par rapport aux notes présentes à un instant donné. Une nouvelle note proposée par le musicien se placera dans l’ensemble des notes existantes de façon la plus harmonieuse, possible comme un atome dans une molécule qui minimise les énergies d’interactions mutuelles, mesurées par la norme |a/b| = ln(ab). Dans cette vidéo, le tempérament adaptatif sont les notes jaunes au voisinage des notes jouées qui sont rouges ou bleues.

Dans ce projet on a un « instrument logiciel de musique juste » qui permet d’utiliser ce tempérament adaptatif sur le réseau tonnetz des intervalles justes pour la composition et prestations musicales sur scène avec une utilisation simple malgré sa définition mathématique un peu abstraite. On utilise des instruments électroniques (claviers MIDI, EWI) mais aussi des instruments acoustiques : une flûte à coulisse commandée par ordinateur qui est accordée en temps réel par un servomoteur pour suivre précisément ce tempérament adaptatif. Il y a aussi des accordeurs visuels à utiliser en direct pour d’autres instruments comme le violon ou la voix.

Voici un exemple d'une improvisation en tempérament adaptatif sur une suite aléatoires d’accords justes, par Malik Mezzadri, Jean Luc Lehr, Maxime Zampieri, Alexandre Ratchov (concert à l’hexagone de mars 2015). Les notes sur le réseau Z^P sont projetées en temps réel.  Il peut paraître étonnant que cette évolution harmonique qui « sonne assez classique », soit seulement basée sur la description mathématique des nombres rationnels dans le réseau tonnetz Z^P  muni d’une norme et sans aucune considération musicale a priori.