Maths & Music #7: Adaptive temperament in just music

“Why do certain notes played together sound harmonious and the chords formed have such varied colors? ” Written in two voices, in this article we present a few aspects of this very rich subject, as well as “ adaptive temperament”, the fruit of a collaboration between a musician and a mathematician.

In today's Western musical system, an octave is a 2/1 frequency ratio, and each octave is divided into 12 equal parts on a logarithmic scale called a semitone, giving the chromatic scale, also known as equal temperament. These twelve notes are called do,do#,re,re#,mi,fa,fa#,sol,sol#,la,la#,si or C,C#,D,D#,E,F,F#,G,G#,A,A#,B. Thus, starting with the frequency of A being f_A= 440 Hz, called the tuning fork, we obtain f_A# = f_A2^1/12= 466 Hz, f_B=f_A2^2/12= 494 Hz and so on.

Just fixed temperaments

In another musical system called just music, notes have mutual frequency ratios that are fractions a/b with small integers a, b. These frequency ratios are also called just (or pure) intervals. The most commonly used are the octave 2/1, the fifth 3/2, the fourth 4/3, the major third 5/4, and so on. And let's not forget the 1/1 unison. This system is fairly universal, as these intervals are perceived as “resonant” for psycho-acoustic reasons [5] [2]. These are the intervals between the voice's harmonics.

A question that must have been asked for millennia: from the infinite number of fractions that exist, which notes should be chosen to make (or tune) a musical instrument with just a few strings? Such a choice of notes is called a fixed temperament. It may be objected that, in practical terms, infinity doesn't exist: the auditory perception of frequencies has a limitation. However, this limitation is very fine, of the order of a hundred different notes per octave, which is enormous and far greater than the chromatic scale of 12 notes per octave. The choice of a fixed temperament is a vast subject and depends on the culture [1, chap.5]. In Senegal, in Mandingo music, a kora is tuned according to various possible choices. Indian music has dozens of different ragas. Arabic music has different maqâms. In Europe, a wide variety of temperaments allowed for a great expressive richness [3].

To illustrate an essential problem encountered with fixed temperaments, the figure below presents the temperaments of Zarlino (1517-1590) and Kepler (1571-1630) and shows that the search for a universal just and fixed temperament is hopeless, like a no go theorem [1, chap.5.10].

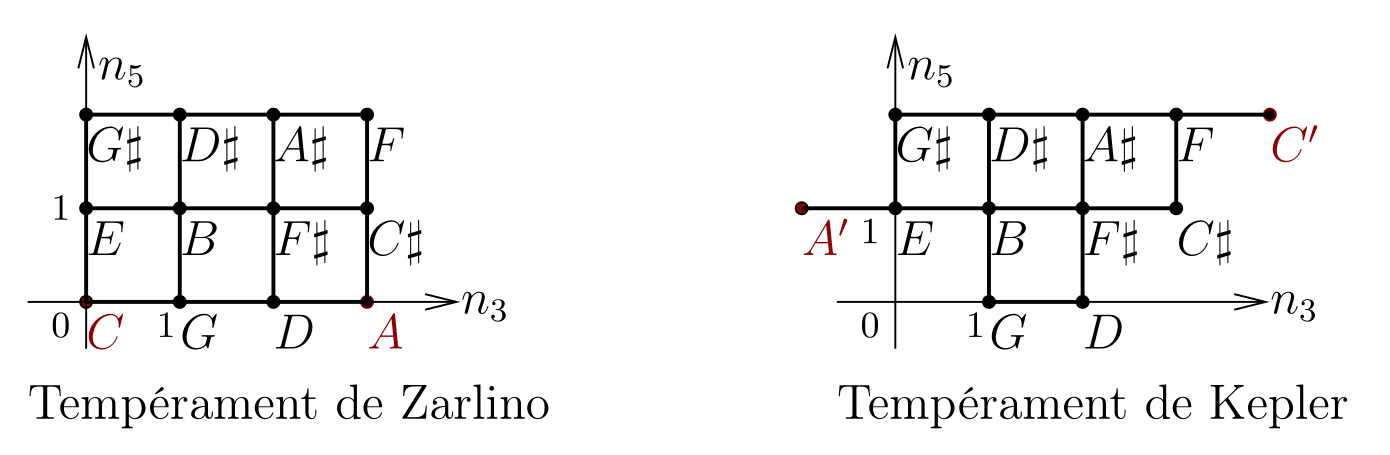
Zarlino or Kepler temperament is the choice of 12 notes per octave (C, C#, D, ..., B) whose relative frequencies are determined by their precise position on a grid with two axes: the fifth axis n₃ and the third axis n₅. More precisely, the frequency f of a note with integer coordinates (n₃,n₅) is f=f_C2ⁿ²3ⁿ³5ⁿ⁵ where the integer depends on the choice of octave and f_C= 262 Hz is the frequency of C (do). Zarlino's temperament contains just fifths such as C --> G and thirds such as C --> E, but does not have the fifths F --> C or A --> E. To obtain these fifths, Kepler modified this temperament by moving the choices C, A to C', A'. In doing so, we lose the fifths C --> G and D --> A and the thirds C --> E and A --> C#. The small deviations called comma are (C-->C') = - 0.20 semitone (dt) and (AA') = - 0.22 dt which are very noticeable. (explanation: = ln(3/2) / ln2^1/12 dt = 7 + 0.02 dt, third = = 4 - 0.14 dt so (CC')=(4 x 0.02-2 x 0.14) dt = - 0.20 dt.)

Equal temperament not right

The impossibility of a temperament that was both just and fixed was seen as a dead end, and led musicians and violin-makers in 19th-century Western music to adopt equal temperament collectively [1, chap.5.14, p.197]: the choice of twelve notes per octave, equally distributed on the logarithmic scale of frequency ratios. The frequency ratio between two notes n semitones apart is 2^n/12, so with a deviation of n = 12 semitones we have the ratio (2^1/12)¹² = 2/1, which is the right octave. But other deviations are not fractions, but irrational numbers. For example, the tritone (3 tones = 6 semitones)= C --> F# est 2^6/12 = the famous irrational number that stirred up trouble in the school of Pythagoras. The strength of this equal temperament lies in the fact that the interval with n = 5 semitones is very close to the right fourth: 2^5/12 = 1.3348... ~ 1,333... = 4/3 and the interval with n = 7 semitones is very close to the perfect fifth: 2^7/12 = 1.498... ~ 1.5 = 3/2 (these deviations are imperceptible to our hearing). Equal temperament was probably adopted because it proposes a construction with intervals of fourths and fifths that are almost exact, and because it is invariant by translation, which corresponds to transpositions in music. However, thirds and other just intervals using the prime numbers 5, 7, 11... will be poorly expressed. Many Western musical movements have sought to “replay” finer intervals, such as just intervals or micro-tonal music.

Right adaptive temperament and right instruments

The adaptive temperament proposed in article [4] enables music to be played with just the right intervals and with only 12 keys per octave: the choice of note pitches is not fixed, but can vary over time and is optimized in relation to the notes present at a given moment. A new note proposed by the musician will fit into the existing set of notes as harmoniously as possible, like an atom in a molecule that minimizes the energies of mutual interactions, measured by the norm |a/b| = ln(ab). In this video, the adaptive temperament is the yellow notes in the vicinity of the notes played, which are red or blue.

In this project, we've developed a “just music software instrument” that makes it possible to use this adaptive temperament on the tonnetz network of just intervals for composition and live performance, in spite of its somewhat abstract mathematical definition. We use electronic instruments (MIDI keyboards, EWI) as well as acoustic instruments: a computer-controlled slide flute that is tuned in real time by a servomotor to precisely follow this adaptive temperament. There are also visual tuners for live use on other instruments such as the violin or voice.

Here's an example of an adaptive temperament improvisation on a random sequence of right chords, by Malik Mezzadri, Jean Luc Lehr, Maxime Zampieri, Alexandre Ratchov (concert at l'hexagone in March 2015). Notes on the ^ZP network are projected in real time. It may seem astonishing that this harmonic evolution, which “sounds quite classical”, is based solely on the mathematical description of rational numbers in the Z^P tonnetz network provided with a norm, and without any a priori musical consideration.